1. 서 론
반도체 소자의 미세화가 지속적으로 진행됨에 따라 구리 인터커넥션 (Cu interconnection)의 치수 역시 비례해서 감소하여 최신 반도체 소자의 인터커넥션 선폭은 구리의 벌크 상태에서의 전자평균이동거리 (electron mean free path, EMFP)인 39 nm보다 더 낮은 수준까지 축소되었다 [1]. 이러한 인터커넥션 치수 감소는 두 가지 중요한 문제점을 야기하게 되었다. 첫번째는 전류밀도와 소자 동작 온도가 상승함에 따라 전기이동(electromigration)이나 응력공극 (stress voiding)에 의한 인터커넥션 소재 신뢰성이 심각하게 훼손된다는 것이다 [2-4]. 두 번째 문제점은 인터커넥션 선폭이 감소함에 따라 구리 인터커넥션의 비저항이 급격하게 증가하는 비저항 크기 효과 (resistivity size effect)이다 [5-9]. 예를 들면, Cu 인터커넥션의 선폭이 10 nm까지 줄어들게 되면 선 (wire) 비저항은 벌크 비저항의 약 10배까지 상승되는 것이 보고될 정도의 심각한 비저항 증가로 인해[10] 반도체 전력소비량과 속도지연을 일으켜 반도체 소자의 성능을 제한하고 지속적인 소자 스케일링을 가로막는 악영향을 미치게 된다.
소재 신뢰성은 열적 활성화 (thermally activated) 메커니즘인 원자 확산에 의해 열화되기 때문에 높은 원자결합력으로 인해 입계확산과 표면확산 속도가 느린 고융점 소재를 사용하는 것이 유리하며, 이러한 이유로 인해 1990년대에 Al (Tm: 933 K) 인터커넥션에서 Cu (Tm: 1358 K) 인터커넥션으로 전환된 후 비약저인 소재 신뢰성 개선이 이루어졌다 [11]. Cu 인터커넥션의 심각한 비저항 크기 효과는 상온에서 39 nm라는 상대적으로 큰 벌크 EMFP을 가지는 것이 주요 원인이며, 이 값은 포논 산란 (phonon scattering)에 의해 결정되어지는 물질 고유의 값이다. Au과 Ag 역시 EMFP이 각각 39 nm와 53 nm로써[12] 매우 긴 값을 가지기 때문에 Cu와 유사하게 매우 심각한 비저항 크기 효과를 보이는 것으로 보고되었다 [13-15]. 소재의 벌크 EMFP와 녹는 점은 물질 고유의 특성이기 때문에, 혁신적인 인터커넥션 특성 개선은 재료의 변경을 통해서만 실현이 가능하며 CMOS (Complementary-Metal-Oxide-Silicon)공정과의 호환성 역시 필수적인 요소이다. Ru과 Co는 짧은 EMFP, 높은 녹는 점, CMOS 호환성으로 인해 최근 차세대 인터커넥션 물질로 주목을 받고 있다 [1,12,16,17]. 실제로 Ru과 Co는 높은 벌크 비저항값에도 불구하고 Cu보다 저감된 비저항 크기 효과로 인하여 충분히 감소된 인터커넥트 치수에서는 Cu보다 낮은 비저항을 보이게 되는 비저항 역전 현상과 더불어 Cu보다 비약적으로 개선된 재료 신뢰성 결과가 보고가 되었다 [16]. 하지만 향후 Ru과 Co 기반의 인터커넥션 기술 개발이 실제 적용되기 위해서는 비저항 크기 효과를 발생시키는 표면 산란과 입계 산란의 비저항 증가분에 대한 정량화 및 산란 파라미터들의 영향력에 대한 분석이 필요하다. 본 연구에서는 Fuchs-Sondheimer 표면 산란 모델과 Mayadas-Shaztkes 결정립계 산란 모델을 이용하여 문헌상 보고된 Ru과 Co의 비저항 크기 효과를 분석하고 나노스케일 인터커넥션에서의 비저항 시뮬레이션을 통해 향후 인터커넥션 개발 방향을 제시하고자 한다.
2. 계산 방법
2.1 산란 모델
박막의 두께나 결정립 크기 등의 치수가 벌크 EMFP와 비슷해질 정도로 감소할 때 비저항이 증가하게 되는 비저항 크기 효과는 J. J. Thomson에 의해 최초로 보고가 되었으며 [18], 그 후 비저항 크기효과에 대해 다수의 물리적 모델들이 제시되었다 [8]. 이 모델들에 의하면 비저항 크기효과는 전기장에 의해 가속된 전자가 산란현상에 의해 초기 운동량을 잃기 때문에 발생하며, 전도체의 두께나 결정립 크기가 감소할 때 비저항이 증가하는 현상적인 사실에 기반하여 표면 산란 (surface scattering)과 입계 산란(grain boundary scattering)이 비저항 크기 효과를 발생시키는 두 가지 주요한 메커니즘으로 제안되었다. 이러한 비저항 크기 효과를 설명하는 데 있어 가장 널리 사용되는 물리적 모델은 Fuchs-Sondheimer (FS) 표면 산란 모델과 [19,20] Mayadas-Shatzkes (MS) 결정립계 산란 모델이며 [21], 두 모델 모두 볼츠만 수송이론 (Boltzmann transport theory)에 기반하여 유도되었다. FS 모델에서는 금속 박막이나 와이어 내의 전도 전자 (conduction electron)가 표면에 충돌 시 전자의 운동량이 보존되어 비저항 증가를 일으키지 않는 거울반사 (specular scattering)와 충돌 시 전자의 운동량을 상실하여 비저항 증가를 일으키는 난반사(diffuse scattering)의 두 경우를 가정하며, 거울 반사를 일으키는 전자의 분율을 표면 거울 반사 마라미터 (surface specular parameter)인 p, 난반사를 일으키는 전자의 분율을 (1-p)로 정의하였다. FS 모델에 의한 박막의 비저항 식은 다음과 같다.
여기서 ρi는 금속의 벌크 비저항, k는 L/λ, L은 박막의 두께, λ는 EMFP이다.
MS 모델 역시 FS 모델과 유사하게 결정립계에서 산란되는 전자의 분율인 반사계수 (reflection coefficient) R을 포함하며, (1-R)은 산란되지 않고 결정립계를 통과하여 비저항의 증가를 일으키지 않는 전자의 분율을 나타낸다. 표면 산란과 결정립계 산란 사이에 상호작용이 없고 박막의 두께가 무한히 두껍다는 가정하에 결정립계 산란에 의한 비저항 식은 다음과 같다.
여기서 α = (λ⁄g)R⁄(1–R)이며, g는 결정립 크기이다. FS 모델과 MS 모델에서 비저항의 크기 효과의 정도를 결정짓는 중요한 치수 파라미터는 벌크 EMFP이며, 이 값이 클수록 비저항 크기 효과가 더욱 더 심각해질 것으로 예측된다.
2.2 비저항 시뮬레이션
본 연구에서의 비저항 시뮬레이션은 Matthiessen의 규칙, 즉 전도체의 비저항은 각각의 비저항 증가성분의 선형 합(linear summation)으로 표현할 수 있다는 아래 관계식에 기반하여 아래 식을 바탕으로 실시하였다 [7,22].
ρtotal=ρo+ΔρMS+ΔρFS.
여기서 ρo는 벌크 비저항이며, ΔρMS와 ΔρFS는 각각 MS 모델과 FS 모델에 의한 비저항 증가분을 의미한다. 시뮬레이션 수행 시 1.8의 종횡비 (aspect ratio)[22] 를 가지는 4개의 표면에서의 전자 산란을 포함하였으며, 결정립 크기는 선폭과 동일하다고 가정하였는 데, 이는 박막의 결정립 크기는 일반적으로 박막의 두께와 비슷하다는 실험적 근거에 기반한 적절한 가정이다 [8,23]. Cu의 인터커넥션 비저항 시뮬레이션 수행 시 Cu의 확산방지막으로 요구되는 고저항 Ta/TaN 이중층의 두께 (2.4 nm)은 제외하였다 [24].
Cu의 경우 기존에 보고된 산란 파라미터 (scattering parameter)인 p=0.52와 R=0.43[7,8]을 이용하여 비저항을 계산하였으며, Ru와 Co의 경우 산란 파라미터에 대한 신뢰도 있는 연구결과의 부재로 인해 Cu의 산란 파라미터를 Ru과 Co에도 동일하게 적용하여 비저항 시뮬레이션을 수행하였을 뿐만 아니라, p, R, 결정립 크기 등의 모델 변수를 인위적으로 변경할 때 비저항 크기 효과에 미치는 영향에 대해서도 분석하였다. 모든 계산은 Mathematica 8.0 (Wolfram)을 이용하여 실시되었다. 표 I에 비저항 시뮬레이션에 활용된 전기적 파라미터를 포함하여 중요한 물질 특성에 대해 정리하였다.
3. 결과 및 고찰
표 1에 정리된 바와 같이 Cu (1358 K)에 비해 훨씬 더 높은 녹는 점을 가지는 Ru (2607 K)과 Co (1768 K)는 인터커넥션 적용 시 비약적으로 향상된 소재 신뢰성을 가지는 것으로 보고되었다 [16]. 따라서 본 연구에서는 전기적인 특성, 즉 FS모델과 MS모델을 바탕으로 Ru과 Co의 비저항 크기 효과를 일으키는 전자 산란 메커니즘에 초점을 맞추고자 한다.
그림 1은 문헌상 보고된 Cu, Ru, Co 박막 비저항의 두께 의존성을 함께 나타내었다. 이 그래프에서 Ru과 Co의 비저항 값은 각각의 논문에서의 후막 비저항값 (thick film resistivity)과 표 1의 벌크 비저항값의 차이를 모든 데이터에서 공제한 후 제시하였다 [24]. 즉, 특정 연구에서 Ru 후막 비저항이 10 μΩ-cm이라면 벌크 비저항값과의 차이인 2.8 μΩ-cm을 모든 측정값에서 공제하였다. 그림 1에서의 비저항 비교에서 확연히 드러나듯이 Ru과 Co는 Cu보다 현저히 저감된 비저항 크기효과를 가지며, 약 10 nm의 박막 두께에서 비저항 역전현상이 발생하는 것으로 확인된다. 하지만 2개의 표면에서 전자 산란이 발생하는 박막의 구조와 달리 직사각형 단면 구조인 인터커넥션은 4개의 표면에서 전자 산란이 발생하기 때문에 인터커넥션 비저항의 증가는 그림 1보다 더욱 더 급격하게 발생할 것으로 예측된다. 뿐만 아니라, Ta/TaN 등 훨씬 더 높은 비저항을 가지는 확산 방지막이 필요한 Cu와 달리 Ru과 Co는 확산방지막이 필요 없기 때문에[25,26] 인터커넥션 구조에서의 비저항 역전 현상은 10 nm보다 상당히 더 큰 선폭에서 발생할 것이라 예측할 수 있다. 이러한 비저항 크기효과 저감효과에 기반하여 최근 Ru과 Co에 대한 인터커넥션 적용 관련 연구결과가 보고되고 있지만[1,16] 그림 1에서 상대적으로 큰 데이터 산란도가 암시하듯이 비저항 크기효과에 직접적인 영향을 미치는 재료의 미세구조에 대한 체계적인 분석이 결여되어 있는 상황이다. 즉, Cu의 경우 27-158 nm 두께 범위의 박막을 성장시키고 각 두께에서 1,000개 이상의 결정립 크기 측정을 바탕으로 비저항 크기효과를 분석한 결과 표면 산란과 결정립계 산란 각각의 메커니즘에 대한 비저항 기여도의 정량적 연구 결과를 보고하였지만[7,8,27], Ru과 Co에 대해서는 이러한 체계적인 연구가 아직까지 진행되지 않은 상황이다.
그림 2에는 문헌상 보고된 Ru과 Co 박막의 비저항값과 FS 모델간의 피팅 결과를 보여준다. 그래프에서 확연히 드러나듯이 FS 모델에 의한 비저항 증가는 가장 극단적인 조건인 p=0인 경우 (100% 표면 난반사)를 가정하더라도 Ru과 Co 박막의 실제 비저항 증가에 미치지 못하게 되며, 이는 표면에서의 전자 산란 현상만으로 Ru과 Co의 비저항 크기효과를 설명하기에는 부족하다는 것을 의미한다. 특히, 약 10 nm 이하의 두께에서는 모델 예측치와 실제 비저항값의 차이가 더욱 더 커진다는 점을 고려할 때, 이 두께 영역에서는 결정립계 산란이 비저항 크기효과를 발생시키는 중요한 메커니즘인 것으로 결론 내릴 수 있다. 하지만 Ru과 Co의 경우 결정립계 반사 계수나 결정립 크기 등 결정립계 산란의 중요 파라미터가 비저항 크기효과에 미치는 영향에 대한 체계적인 연구가 수행되지 않은 상황이다. 따라서 본 연구에서는 MS 모델을 이용한 Ru과 Co 인터커넥션의 비저항 시뮬레이션을 수행하였으며 그 결과를 바탕으로 Ru과 Co의 차세대 인터커넥션 적용성에 대한 가능성을 제시하고자 한다.
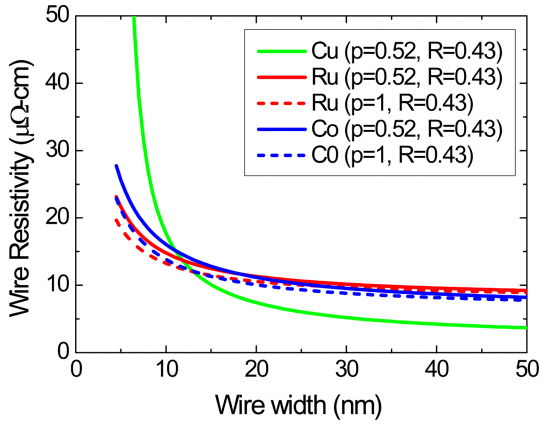
Cu보다 벌크 비저항이 높지만 현저히 짧은 EMFP를 가지는 Ru과 Co를 적용한 차세대 인터커넥션 개발을 위하여 중요한 평가 항목중의 하나는 Ru과 Co가 Cu 인터커넥션과 비슷한 나노스케일의 선폭을 가질 때의 비저항을 비교하는 것이다. 그림 3은 FS 모델과 MS 모델을 이용하여 수행한 와이어 비저항 시뮬레이션 결과를 나타내었다. 그 결과 Ru과 Co의 비저항 역전 현상은 11-12 nm 선폭에서 발생하였다. 표면 산란의 심각도를 확인하기 위하여 그림 3에는 표면 산란에 의한 비저항 증가가 발생하지 않는 p=1 (100% 거울 반사)을 가정한 조건에서의 모델 시뮬레이션 결과와 비교할 때, 상대적으로 급격한 비저항의 감소는 발생하지 않았다. 본 시뮬레이션에서 주목할 점은 일단 비저항 역전 현상이 발생하면 그 이하 선폭에서는 Cu와 Ru/Co의 비저항 차이가 급격하게 증가하게 되며 이는 그림 1에서의 실험 결과와도 전반적으로 일치한다.
산란 모델의 분석 결과 Ru와 Co 인터커넥션의 지배적인 산란 메커니즘으로 밝혀진 결정립계 산란현상의 반사계수(R)와 결정립 크기 (g)가 비저항 크기 효과에 미치는 영향에 대해 분석을 실시하였다. 먼저 그림 4(a)-(b)에서는 p를 0.52로 고정한 채 결정립 크기가 선폭과 동일하다고 가정하며 R을 0.2-0.43 구간 내에서 변화시키면서 비저항 시뮬레이션을 수행하였으며, 그 결과 그림 3에서 밝혀진 p의 변화보다 R의 변화가 비저항 크기효과에 미치는 영향이 훨씬 더 크다는 것을 보여준다. 예를 들어, R=0.2의 경우 비저항 역전 현상은 16 nm (Ru)과 17 nm (Co)의 선폭에서 각각 발생하게 된다. 또 다른 산란 파라미터인 결정립의 크기에 대한 효과를 파악하기 위하여, p=0.52와 R=0.43은 그림 4(a)-(b)와 동일하게 유지한 채 결정립 크기를 선폭의 2-4배까지 변화시키면서 실시한 계산 결과를 그림 4(c)-(d)에 나타내었다. 결정립 크기가 선폭의 2배로 증가될 때는 현저한 비저항 감소로 이어졌으나 추가적인 결정립 크기 증가는 소폭의 비저항 감소만이 발생 하였는 데 이는 결정립 크기가 Ru과 Co의 bulk EMFP보다 상대적으로 커지기 때문에 비저항 크기 효과가 제한적으로 나타나는 것이라 해석할 수 있다. 표 II에 산란 파라미터 (p & R) 및 결정립 크기 변화가 Ru과 Co 인터커넥션의 비저항 크기효과에 미치는 영향에 대해 분석한 결과를 정리하였다.
FS 모델과 MS 모델을 이용하여 Ru과 Co 인터커넥션의 비저항 시뮬레이션 분석 결과, 두 물질 모두 나노스케일에서 Cu 인터커넥션보다 낮은 비저항을 가지게 되는 비저항 역전 현상이 발생할 것으로 예측되며, 이 시뮬레이션 결과는 그림 1의 문헌상 보고된 박막의 비저항 크기 효과 데이터와 유사한 경향을 보인다. 또한 Ru과 Co의 경우 전자의 표면 산란을 제어하는 것보다 결정립을 조대화하거나 결정립계 산란 파라미터를 낮추는 접근 방법이 인터커넥션의 비저항 크기 효과를 저감시키는 데 훨씬 더 효과적일 것으로 예측된다. 특히, 결정립 크기 증가에 따른 현저한 비저항 감소 현상은 Cu와 W에서 실험적으로도 확인되었다는 점은 주목할 만하다 [7,8,38]. 결정립계에서 원자 산란이 발생하는 근본적인 이유가 원자의 주기적인 포텐셜이 흐트러져 있는 무질서도 기인한다는 점에 근거한다면 동일한 재료라도 결정립계 산란 파라미터는 결정립계의 무질서도, 즉 인접 결정립계간의 경사각 (tilted angle) 및 회전각(twisted angle)에 영향을 받을 것으로 기대된다. 따라서 결정립계의 무질서도가 낮은 저각 경계 (low-angle grain boundary)를 형성하는 공정 개발 등을 통해 R값을 낮추는 접근방법 및 결정립 조대화 공정개발 등이 효과적인 비저항 저감 방안이 될 것으로 예측되며, 이러한 목표 달성을 위한 실험적인 노력이 필요하다. 뿐만 아니라, Ru과 Co 이외에도 짧은 EMFP를 가지는 타 금속 소재를 이용한 미래 반도체 인터커넥션 적용연구 역시 필요하다고 판단된다.
4. 결 론
본 연구에서는 Ru과 Co의 차세대 반도체 인터커넥션 적용 가능성에 대해 논하였다. 현재 인터커넥션 물질로 사용되고 있는 Cu의 전자평균이동 거리인 39 nm보다 훨씬 더 짧은 값을 가지는 Ru (6.6 nm)와 Co (11.8 nm)은 상대적으로 높은 비저항에도 불구하고 저감된 비저항 크기효과와 향상된 물질 신뢰성을 가질 것으로 예측되어 차세대 인터커넥션 물질로 주목을 받고 있다. 본 연구에서는 Fuchs-Sondheimer 표면 산란 모델과 Mayadas-Shatzkes 결정립계 산란 모델에 기반하여 Ru과 Co의 차세대 인터커넥션 적용성에 대한 연구를 수행하였다. 문헌상 보고된 Ru과 Co의 비저항 크기 효과 데이터를 분석한 결과 결정립계 산란 현상이 Ru과 Co의 비저항 증가의 지배적인 메커니즘으로 밝혔다. 산란 모델의 주요 파라미터 변화에 따른 비저항 시뮬레이션을 통한 수행한 결과 Ru과 Co 인터커넥션은 약 15 nm 선폭에서 Cu보다 낮은 비저항을 보이는 비저항 역전 현상을 보일 것으로 예상된다. 향후 실험적인 산란 파라미터 검증과 더불어 결정립 조대화, 산란 파라미터 저감 공정 개발 등을 통해 Ru/Co 인터커넥션의 성능을 극대화하는 노력이 필요할 것으로 전망한다.