Recently, there has been growing interest in various industries in energy harvesting technologies that use waste heat, and thermoelectric materials are being actively studied for that application because of their advantages, including eco-friendliness and low noise [1,2]. Because thermoelectric materials can directly convert waste heat into electricity, their energy use efficiency can be increased. The performance of thermoelectric materials is determined by the dimensionless figure of merit zT = S²σT/κ_tot, where S, σ, T, and κ_tot are the Seebeck coefficient, electrical conductivity, absolute temperature, and total thermal conductivity, respectively. Therefore, to improve zT, S and σ should be en_Hanced, whereas κ_tot should be reduced [3-6].

Oxide thermoelectric materials have attracted significant attention over the past few decades owing to their potential applications at high temperatures without a protective atmosphere, and excellent thermal and chemical durability [7-9]. However, because of their high thermal and low electrical conductivities, the thermoelectric performance of oxides in commercial applications is very poor. Recently, BiCuSeO, a p-type oxyselenide material, has attracted the attention of many researchers. Composed of alternate stacks of conducting layer [Cu₂Se2]²⁻ and insulating layer [Bi₂O₂]²⁺, BiCuSeO has an intrinsically low thermal conductivity [10]. A maximum zT of ~1.5 was achieved for BiCuSeO, which indicates that it can be used as a p-type thermoelectric module for thermoelectric devices [11]. Bi₂O₂Se can be considered an n-type counterpart of the p-type BiCuSeO. This is because, similar to BiCuSeO, Bi₂O₂Se consists of alternately stacked insulating [Bi₂O₂]²⁺ layers and conducting [Se]²⁻ layers. The [Bi₂O₂]²⁺ layers can be considered phonon scattering regions, while the [Se]²⁻ layers provide conduction pathways for electrons [12]. Bi₂O₂Se has a large S and intrinsically low thermal conductivity; however, because of its low carrier concentration and σ, the thermoelectric performance of Bi₂O₂Se is limited [13]. Recent studies have been conducted to improve the electrical transport properties of Bi₂O₂Se by various strategies, such as anion doping, cation doping, Ag addition, and Bi deficiency [14-19].

In this study, we investigated the thermoelectric properties of Cu-doped Bi₂O₂Se. The weighted mobility (μ_w) and quality factor (B) were calculated to validate the optimization of the power factor and zT.

Cu_xBi₂O₂Se (x = 0, 0.0025, 0.005, and 0.0075) polycrystalline samples were synthesized by a solid-state reaction using high-purity raw materials. Stoichiometric amounts of Bi (99.99%, KRTLab), Se (99.999%, 5N Plus), Bi₂O₃ (99.99%, Alfa Aesar), and Cu (99.999%, KRTLab) powders were weighed and mixed. The mixed raw materials were placed in a quartz tube and vacuum sealed. After melting at 600°C for 24 h, the mixture was cooled in a furnace to prepare an ingottype synthesized sample. The synthesized samples were ground into powder using a high-energy ball mill (SPEX 8000D, SPEX, USA). The samples were sintered by spark plasma sintering (SPS, SPS-1030, Sumitomo Coal Mining Co., Ltd., Japan) at 873 K for 10 min under a pressure of 50MPa. The relative densities of all sintered samples were over ~96%. X-ray diffraction analysis (XRD, D8 Discover, Bruker, USA) using Cu K_α1 radiation was performed to identify the phase formation behavior and the presence of a secondary phase. The σ and S values of each sample were measured using a thermoelectric evaluation system (ZEM-3M8, Advance Riko, Japan), under an atmosphere of He in the range of 300-800 K. The error margins for σ and S were less than 3% and 5%, respectively. Hall measurements were conducted in the Van der Pauw configuration using a Hall measurement system (HMS-5300, Ecopia, Korea) at 300 K. Using the Mott relationship, the density-of-state effective mass (m_d^*) of each sample was calculated from S and Hall carrier concentrations. The thermal conductivity (κ_tot) of each sample was determined using the relationship κ_tot = αρC_p, where α, ρ, and C_p are the thermal diffusivity, density, and heat capacity, respectively. The α value of each sample was measured using laser flash analysis (LFA, LFA457, Netzsch, Germany) from 300 to 800 K. The error margin for α was less than 7%.

We assumed that ρ and C_p were constant regardless of the addition of Cu, where ρ is the theoretical density of Bi₂O₂Se [20]. Because the amount of added Cu was very small, changes in the density and heat capacity due to the addition were considered negligible.

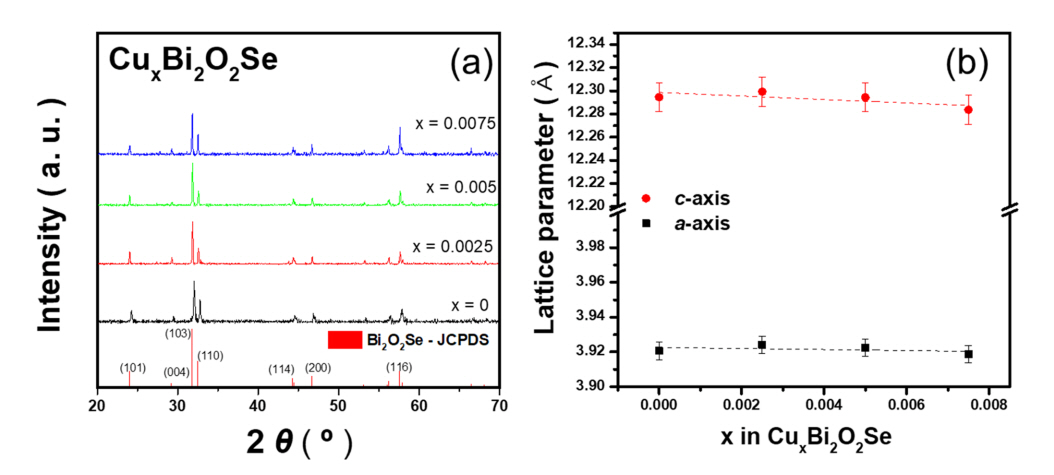
Figure 1(a) presents the XRD patterns of a series of Cudoped Bi₂O₂Se polycrystalline powder samples (Cu_xBi₂O₂Se, x = 0, 0.0025, 0.005, and 0.0075) at 300 K. As shown in Figure 1(a), tetragonal Bi₂O₂Se (Bi₂O₂Se, JCPDS #070-1549) was successfully synthesized. Figure 1(b) shows the calculated lattice parameters a and c from the XRD results with error bars. The (0 0 4) peak was used to calculate lattice parameter c, and the lattice parameter a was extracted from the (1 0 1) peak. The lattice parameters gradually decreased with Cu addition; however, significant differences were not observed between the samples (the variation between lattice parameters of the samples was within 0.2%). The gradual decrease in lattice parameters indicates that the added Cu atoms were successfully substituted at the Bi site. This is because of the difference in electronegativity; the electronegativity values of Cu, Bi, Se, and O are 1.90, 2.02, 2.55, and 3.44, respectively. In addition, if the added Cu atoms were interstitially doped, the lattice parameter would gradually increase. This evidence supports the substitution of Bi and Cu.

Figure 2(a) shows the temperature dependence of σ for the Cu_xBi₂O₂Se (x = 0, 0.0025, 0.005, and 0.0075) samples. At 300 K, σ of the pristine Bi₂O₂Se sample was 16.0 S/cm and it decreased to 12.8, 7.10, and 0.23 S/cm for x = 0.0025, 0.005, and 0.0075, respectively. At 790 K, σ of the pristine Bi₂O₂Se sample was 22.6 S/cm, and it decreased to 18.6, 10.1, and 4.81 S/cm for x = 0.0025, 0.005, and 0.0075, respectively. The σ value gradually decreased with increasing Cu content.

Figure 2(b) shows the measured S values as a function of temperature for the samples. At 300 K, the S value of the pristine Bi₂O₂Se sample was -232 μV/K, which improved to -288, -280, and -377 μV/K for x = 0.0025, 0.005, and 0.0075, respectively. At 790 K, the S value of the pristine Bi₂O₂Se sample was -316 μV/K, which improved to -328, -362, and -443 μV/K for x = 0.0025, 0.005, and 0.0075, respectively. The magnitude of S generally increased with increasing x over the entire temperature range. The band gap E_g of the samples was estimated from the maximum magnitude of the Seebeck coefficient, |S|_max and the corresponding temperature T_max, using the Goldsmid-Sharp empirical equation E_g = 2e|S|_maxT_max [21] and are listed in Table 1. The estimated E_g values of the samples gradually increased with x, suggesting that carrier excitation was suppressed by the addition of Cu.

Figure 2(c) shows the calculated power factor of the samples as a function of temperature. The highest power factors were observed for the pristine Bi₂O₂Se sample in the high-temperature range. However, in the low-temperature range, the sample with x = 0.0025 exhibited the highest power factor value. Consequently, the power factor for the pristine Bi₂O₂Se sample of 0.086 mW m^-1 K^-2, which improved to 0.106 mW m^-1 K^-2 for x = 0.0025 at 300 K. However, the power factors of the other Cu-added samples decreased compared to that of the pristine sample, mainly owing to the significant decrease in σ. The contribution of the increase in the magnitude of S to the power factor was canceled out by the decrease in σ for these samples.

The Hall carrier concentration (n_H) was measured at 300 K and is shown in Figure 3(a). The n_H value of the pristine Bi₂O₂Se sample was -2.11 × 10¹⁸ cm^-3 and changed to -8.95 × 10¹⁷, -4.81 × 10¹⁷, and -2.37 × 10¹⁷ cm^-3 for x = 0.0025, 0.005, and 0.0075, respectively. The n_H value decreased exponentially with increasing Cu content. This result is in accordance with the band gap estimated using the Goldsmid-Sharp equation. Generally, electron carrier excitation is restricted to large-bandgap materials. Furthermore, n_H is closely related to S according to the Mott relationship [22].

where k, h, e, and n are the Boltzmann constant, Planck’s constant, elementary charge, and carrier concentration, respectively. Generally, an increase in |S| is expected as n decreases, because |S| and n are inversely proportional to each other. Therefore, the increase in |S| was mainly attributed to the decrease in n_H. The Hall mobility (μ_H) was measured at 300 K, as shown in Figure 3(b). The μ_H values of the samples were 53.3, 106, 120 and 48.6 cm²/Vs for x = 0, 0.0025, 0.005, and 0.0075, respectively. The μ_H values increased up to x = 0.005 but decreased at x = 0.0075.

Figure 3(c) shows |S| as a function of n_H (Pisarenko plot). The inset in Figure 3(c) shows m_d^* calculated from n_H and S measured at 300 K for the Mott relationship in Equation (1) as a function of x in Cu_xBi₂O₂Se (x = 0, 0.0025, 0.005, and 0.0075). The dotted lines in Figure 3(c) indicate the Mott relationship functions, wherein, m_d^* were calculated as variables, for the Cu-added Bi₂O₂Se. The m_d^* value was highest at 0.190 m₀ (m₀ is the electron rest mass) for pristine Bi₂O₂Se and gradually decreased with the addition of Cu to 0.133, 0.0858, and 0.0718 m₀ for x = 0.0025, 0.005, and 0.0075, respectively. The continuous decrease in m_d^* with the Cu addition implies that the band structure was unfavorably modified by the Cu addition.

Figures 4(a) and 4(b) show κ_tot and lattice thermal conductivity (κ_lat) as a function of temperature for the Cu_xBi₂O₂Se (x = 0, 0.0025, 0.005, and 0.0075) samples. The inset of Figure 4(a) shows the electronic thermal conductivity (κ_ele) of the samples, calculated using the Wiedemann-Franz law [23]: κ_ele = LσT, where L is the Lorenz number. The κ_lat value was obtained by subtracting κ_ele from κ_tot. Because the electronic contribution to κ_tot was considerably small (the measured σ was less than 30 S/cm), κ_tot and κ_lat exhibited almost identical values. The κ_tot and κ_lat values for the Cucontaining samples were lower than those of the pristine Bi₂O₂Se sample. The κ_lat values of the samples were 1.59, 1.31, 1.31, and 1.16 W/mK at 300 K and 0.829, 0.690, 0.699 and 0.680 W/mK at 790 K for x = 0, 0.0025, 0.005, and 0.0075, respectively. Further, κ_lat generally decreased with an increase in Cu content, which is due to point defect phonon scattering via Cu addition. The decrease in the lattice parameters a and c for the Cu-added samples implies lattice distortion in their crystal structure, which contributed to the decrease in κ_lat.

Figure 5(a) shows the temperature dependence of zT for the Cu_xBi₂O₂Se (x = 0, 0.0025, 0.005, and 0.0075) samples, calculated using the σ, S and κ_tot values. The zT value, en_Hanced from 0.206 to 0.222 for x = 0.0025 compared to that of the pristine Bi₂O₂Se sample at 790 K, owing to a decrease in κ_tot and a small change in the power factor. Note that the error margin for zT would be less than 15%. However, the zT value of the other Cu-added samples decreased compared with that of the pristine sample, mainly because of the large decrease in the power factor. Consequently, a maximum zT of 0.222 at 790 K was obtained for the sample with x = 0.0025.

The weighted mobility (μ_w) of each sample was calculated using the measured σ and S, as shown in Figure 5(b). The μ_w value is theoretically related to the maximum electrical performance of the thermoelectric material. Further, μ_w can be calculated from an analytical expression that estimates the exact Drude-Sommerfeld free electron model for |S| > 20 μV/ K [23]:

where m_e is the mass of the electron. At 300 K, the μ_w values of the samples were 10.5, 15.3, 7.95, and 0.794 cm²/Vs for x = 0, 0.0025, 0.005, and 0.0075, respectively. The μ_w value increased initially for x = 0.0025 and decreased with Cu content for x = 0.005 and 0.0075, closely following the power factor trend at 300 K. The power factor for x = 0.0025 at 300 K increased only by ~23%, and it can be further improved by appropriate n_H tuning. Figure 5(c) shows the dimensionless B of each sample determined from μ_w and κ_lat. The B value of each sample was calculated as follows [23]:

B is relative to the maximum zT that can be achieved when n_H is optimized [24,25]. The values of B at 300 K were 0.00450, 0.00862, 0.00434, and 4.91 × 10^-4 for x = 0, 0.0025, 0.005, and 0.0075, respectively. The B value increased at x = 0.0025 and then decreased with the addition of Cu, which is in accordance with the zT trend at 300 K. In addition, the sample with x = 0.0025 exhibited a maximum B value of 0.0964 at 790 K, and the power factor improvement for x = 0.0025 could be greatest at 790 K. Therefore, further enhancement of zT can be achieved by optimizing n_H for the Cu_0.0025Bi₂O₂Se (x = 0.0025) composition.

Figure 5(d) presents the calculated n_H-dependent zT for Cu_xBi₂O₂Se (x = 0, 0.0025, 0.005, and 0.0075) at room temperature. The experimental zT measurements are indicated by symbols. The theoretical peak zT of the Cudoped samples estimated using the single parabolic band model was significantly greater than that of the Bi₂O₂Se sample [26]. Among the doped samples, the theoretical zT of Cu_0.0025Bi₂O₂Se was the highest in all n_H regions. The zT value of Cu_0.0025Bi₂O₂Se can be further improved by tunning n_H from 8.9 × 10¹⁷ to 4.7 × 10¹⁸ cm^-3. For instance, the zT of the Cu_0.0025Bi₂O₂Se sample can reach 0.034 at n_H of approximately 4.7 × 10¹⁸ cm^-3, which is approximately 36% higher than that of 0.025 at 300 K.

In this study, we investigated the electrical transport and thermoelectric properties of Cu-doped n-type Bi₂O₂Se (Cu_xBi₂O₂Se with x = 0, 0.0025, 0.005, and 0.0075). Tetragonal Bi₂O₂Se was successfully synthesized, and the lattice parameters a and c gradually decreased with Cu addition. Over the entire temperature range, σ gradually decreased and the magnitude of the S gradually increased with increasing x content, according to the trade-off relationship between the parameters. Consequently, at 300 K, a maximum power factor of 0.106 mW m^-1 K^-2 was obtained for the sample with x = 0.0025, owing to the increase in the magnitude of S. The Hall carrier concentration decreased exponentially with increasing Cu content, which is mainly attributed to the possible enlargement of the band gap of the Cu-added samples. The κ_lat value decreased with increasing x, which was attributed to the point defect phonon scattering caused by the Cu addition. Therefore, a maximum zT of 0.222 was achieved at 790 K for the Cu_0.0025Bi₂O₂Se (x = 0.0025) sample, which was approximately 8% higher than that of the pristine Bi₂O₂Se sample.