Synthesis and Thermoelectric Properties of Partially Double-Filled Skutterudites (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂

Article information

Abstract

1. INTRODUCTION

Thermoelectricity is a technology that directly converts thermal energy into electrical energy or electrical energy into thermal energy. The thermoelectric conversion efficiency is evaluated by a dimensionless figure of merit, ZT = α²σκ⁻¹T, where α is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and Τ is the absolute temperature [1]. Two main methods are used to improve ZT and obtain high conversion efficiency. The first is to increase the power factor (α²σ) and the second is to decrease the thermal conductivity. The thermal conductivity is composed of two contributions: lattice thermal conductivity (κ_L) and electronic thermal conductivity (κ_E). These components can be separated using the Wiedemann-Franz law (κ_E = LσT), where L is the Lorenz number [2]. As the carrier concentration increases, the electrical conductivity and electronic thermal conductivity increase, but the Seebeck coefficient decreases. Specifically, because the power factor has a trade-off relationship between the electrical conductivity and Seebeck coefficient, the reduction in thermal conductivity should be achieved through the reduction in lattice thermal conductivity. However, the parameters cannot be controlled independently because the thermal conductivity increases along with the electrical conductivity [3,4].

Skutterudite has a body-centered cubic structure with the space group Im3, and its unit cell is assembled in the form of 8MX₃ with 32 atoms, where M is the transition element and X is the pnicogen element [5]. There are two voids per unit cell of the skutterudite, and p-type RFe₄Sb₁₂-based and n-type RCo₄Sb₁₂-based filled skutterudites have been studied, where R is the rattler filled with alkali, alkaline-earth, or rare-earth atoms. The filled skutterudite induces phonon scattering of rattlers in the lattice to reduce the lattice thermal conductivity [6,7]. However, similar to RFe₄Sb₁₂, it is difficult to obtain a high thermoelectric performance as the hole concentration is very high and the Seebeck coefficient is relatively low. In addition, [Fe₄Sb₁₂] is unstable owing to deficient valence electrons, thus four electrons are required to stabilize the skutterudite phase [8]. The skutterudite can be stabilized in the form R⁴⁺[Fe₄Sb₁₂]⁴⁻ by filling the voids with R⁴⁺ ions; however, most elements used as fillers exist with valences of R²⁺ and R³⁺, as a result, the valence electrons are insufficient [9]. Thus, charge compensation is required and this is fulfilled by substituting Co or Ni at the Fe site [10]. Several studies on phase stabilization and improved thermoelectric performance of the p-type RFe₄Sb₁₂ have been reported, and the thermoelectric properties may be enhanced by reducing the lattice thermal conductivity through single or multiple fillings with charge compensation [11-14]. In particular, filling two or more rare-earth elements with heavy atomic masses greatly reduces the lattice thermal conductivity through phonon scatterings with lower and broader resonance frequencies [6,15,16]. In this study, we prepared p-type (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂ with partial double filling of La/Yb and substitution of Co at the Fe site and examined their thermoelectric properties.

2. EXPERIMENTAL PROCEDURE

Elemental La (purity 99.9%, Kojundo), Yb (purity 99.9%, Sigma Aldrich), Co (purity 99.95%, Alfa Aesar), Fe (purity 99.95%, Cerac), and Sb (purity 99.999%, LTS) were weighed according to the stoichiometric compositions of (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂ (z = 0.25−0.75 and x = 0−1), and melted at 1323 K for 10 h in an evacuated quartz ampoule that was coated inside with carbon followed by water quenching. The obtained ingot was vacuum-sealed and annealed at 873 K for 24 h. The ingot was ground into powder with a particle size of less than 75 μm. The powder was then charged in a graphite die and consolidated by hot pressing at 873 K for 1 h under 70 MPa.

The phases of the hot-pressed bodies were analyzed using X-ray diffraction (XRD; Bruker, D8-Advance) with Cu-K_α radiation in the θ-2θ mode. Microstructures were observed using scanning electron microscopy (SEM; FEI, Quanta400), and atomic distributions were analyzed using energy dispersive spectroscopy (EDS; Oxford, JSM-5800). The electrical conductivity and Seebeck coefficient were simultaneously measured using the DC four-probe method with ZEM-3 (Ulvac-Riko) equipment. The thermal conductivity was evaluated from the measured thermal diffusivity, specific heat, and density using the laser flash method with TC-9000H (Ulvac-Riko) system. The measured Seebeck coefficient, electrical conductivity, and calculated thermal conductivity were used to evaluate the power factor and dimensionless ZT.

3. RESULTS AND DISCUSSION

XRD patterns of the (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂ skutterudites are presented in Fig 1. The diffraction patterns were in good agreement with the standard diffraction data (PDF# 56-1123) for the skutterudite phase, and a small quantity of the marcasite phase (PDF# 70-3985) was identified. The diffraction peaks for the marcasite phase between 30.9° and 32.1° are enlarged in Figs 1(b) and 1(c). The intensity of peak decreased with increasing Co substitution (x); this indicates that the skutterudite phase was stabilized by Co charge compensation. In addition, the diffraction peaks shifted to higher angles with increasing Co content because the smaller Co (atomic radius: 0.167 nm) was substituted for the larger Fe (atomic radius: 0.172 nm) site, which is consistent with the previous studies [17-19].

Fig. 1.

XRD patterns of (a) the (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂ skutterudites and enlarged patterns of the specimens with (b) z = 0.25 and (c) z = 0.75.

Figure 2 displays the SEM images and EDS analyses of (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂ skutterudites. The secondary phase was observed along with the main skutterudite phase; however, less secondary phase was observed with increasing Co substitution. This was consistent with the XRD results. Charge compensation was confirmed to stabilize the skutterudite phase and suppress the formation of the secondary phase. In a previous study [20], the marcasite phase was observed in fully-filled La_1-zYb_zFe4-xCo_xSb₁₂ skutterudites with x ≤ 0.5. However, in this study, the marcasite phase was detected in all specimens, which was because the charge compensation was not sufficiently performed owing to the partial filling with low valence ions of La³⁺ and Yb^2+/3+ [21].

Fig. 2.

SEM images and EDS line scans of (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂.

Chemical compositions, relative densities, and lattice constants of the (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂ are summarized in Table 1. After the completion of the preparation processes, the actual composition showed no significant difference from the nominal composition, and hot-pressed specimens showed relative densities higher than 97.4% compared to the theoretical density. The calculated lattice constant ranged from 0.9129 to 0.9142 nm, and it decreased with increasing amount of La filling and Co substitution because the ionic radii are Fe (0.172 nm), Co (0.167 nm), La (0.136 nm), and Yb (0.139 nm) [22].

Table 1.

Chemical compositions, relative densities, and lattice constants of (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂.

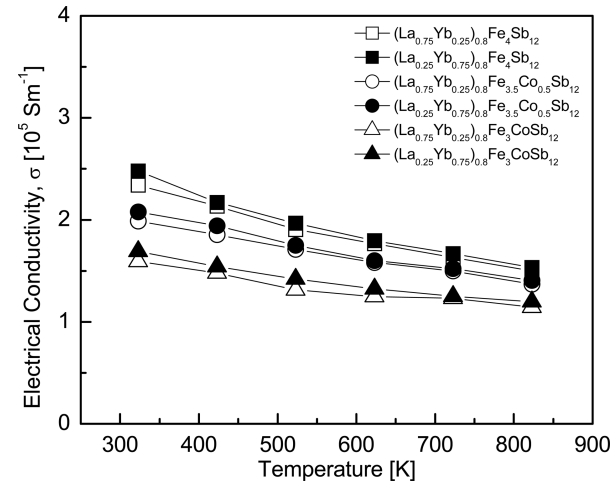
Figure 3 presents the temperature dependence of electrical conductivity for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂. All specimens showed degenerate semiconductor behavior with decreasing electrical conductivity as the temperature increased. Lower electrical conductivity was obtained with increasing La filling and Co substitution. This resulted from the reduction in the carrier concentration caused by the difference in valences of La/Yb and the charge compensation of Co. (La_0.25Yb_0.75)_0.8Fe₄Sb₁₂ showed the highest electrical conductivity of 2.48 × 10⁵ Sm^-1 at 323 K. The fully-filled La_0.25Yb_0.75Fe_3.5Co_0.5Sb₁₂ exhibited a maximum electrical conductivity of 2.08 × 105 Sm^-1 at 323 K [20]; however, in this study, the partially-filled (La_0.25Yb_0.75)_0.8Fe_3.5Co_0.5Sb₁₂ demonstrated higher electrical conductivity than the fully-filled specimens.

Fig. 3.

Temperature dependence of the electrical conductivity for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂.

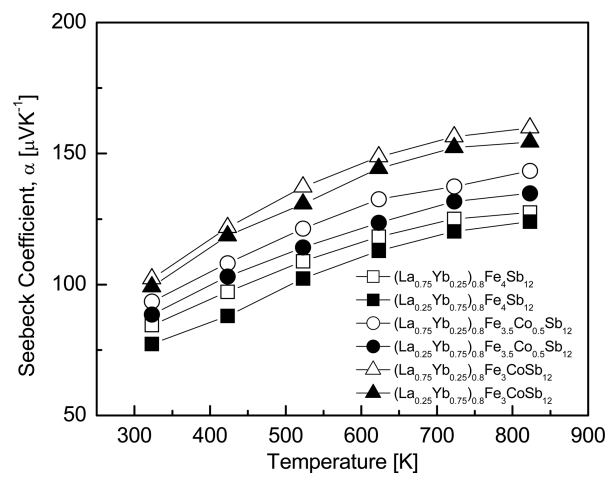
The temperature dependence of the Seebeck coefficient for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂ is shown in Fig 4. All specimens displayed positive values of p-type conductions. The Seebeck coefficient increased as the temperature increased, and it further increased with increasing La filling and Co substitution. This was due to the increased electron donation by Yb and the enhanced charge compensation by Co. (La_0.75Yb_0.25)_0.8Fe₃CoSb₁₂ yielded the highest Seebeck coefficient of 159.7 μVK^-1 at 823 K, and the fully-filled La_0.75Yb_0.25Fe₃CoSb₁₂ exhibited a maximum Seebeck coefficient of 175.5 μVK^-1 at 723 K [20]. Thus, the partially-filled specimens showed lower Seebeck coefficient values than the fully-filled specimens with lower carrier concentrations.

Fig. 4.

Temperature dependence of the Seebeck coefficient for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂.

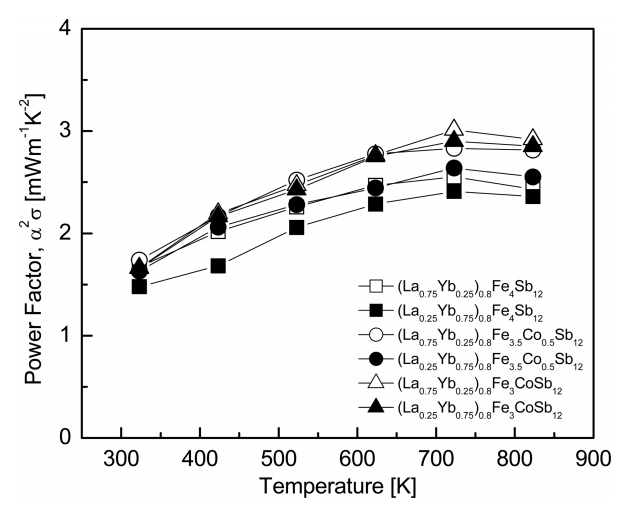
Figure 5 presents the variations of the power factor with temperature and composition for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂. As the temperature increased, the power factor increased and reached the maximum value at 723 K. Higher power factor values were obtained with increasing La filling and Co substitution. However, the difference in the La/Yb filling ratio did not significantly affect the power factor. (La_0.75Yb_0.25)_0.8Fe₃CoSb₁₂ exhibited maximum power factor of 3.01 mWm^-1K^-2 at 723 K, which was higher than the power factor of 2.42 mWm^-1K^-2 at 723 K of the fully-filled La_0.75Yb_0.25Fe₃CoSb₁₂ [20].

Fig. 5.

Temperature dependence of the power factor for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂.

The temperature dependence of the thermal conductivity for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂ is shown in Fig 6. The total thermal conductivity is shown in Fig 6(a). The thermal conductivity apparently decreased with increasing Co substitution, and it was slightly lowered with increasing La filling. The increased thermal conductivity at temperatures above 623 K was due to the bipolar effect. (La_0.75Yb_0.25)_0.8Fe₃CoSb₁₂ showed the lowest thermal conductivity of 2.08 Wm^-1K^-1 at 323 K, and the value was lower than 2.20 Wm^-1K^-1 at 523 K of the fully-filled La_0.75Yb_0.75Fe₃CoSb₁₂ [20].

Fig. 6.

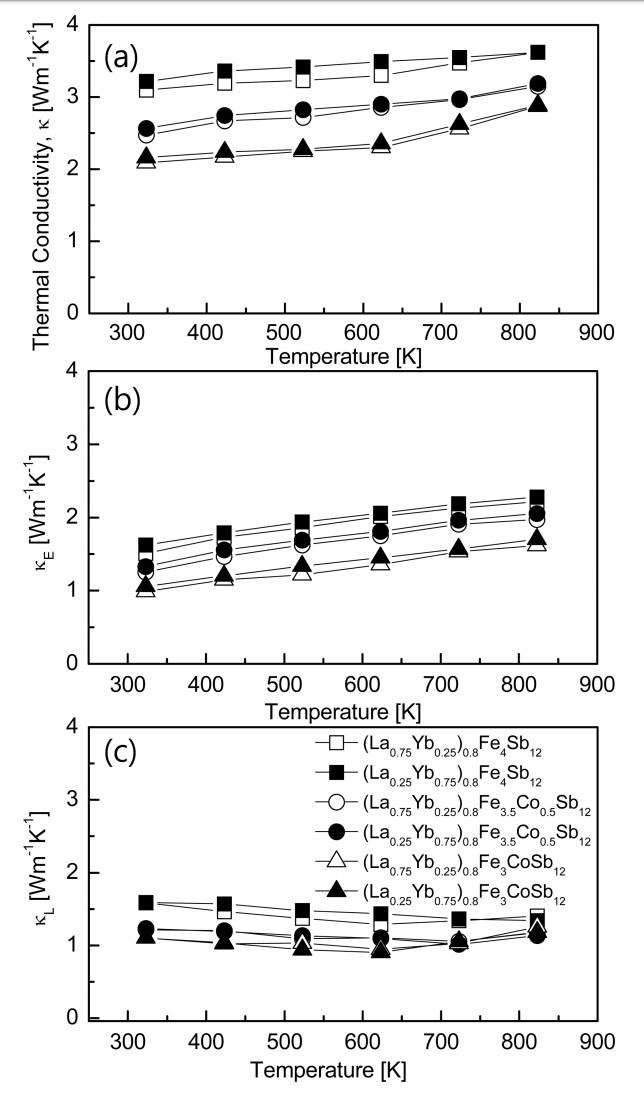
Temperature dependence of the thermal conductivity for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂: (a) total thermal conductivity, (b) electronic thermal conductivity, and (c) lattice thermal conductivity.

The electronic thermal conductivity is shown in Fig 6(b). The Lorenz number was assumed to be 2.0 × 10^-8 V²K^-2. The electronic thermal conductivity decreased with increasing La filling and Co substitution with the same tendency as that of the total thermal conductivity. (La_0.75Yb_0.25)_0.8Fe₃CoSb₁₂ showed the lowest electronic thermal conductivity of 0.98 Wm^-1K^-1 at 323 K. The lattice thermal conductivity is shown in Fig 6(c). The lowest values of κ_L = 0.91‒1.34 Wm^-1K^-1 were achieved in the temperature range of 623‒823 K. No significant change in the lattice thermal conductivity was found by varying the La/Yb filling ratio, but the lattice thermal conductivity decreased with increasing Co substitution. This was due to the enhanced phonon scattering caused by the impurity scattering. (La_0.25Yb_0.75)_0.8Fe₃CoSb₁₂ showed the lowest lattice thermal conductivity of 0.91 Wm^-1K^-1 at 623 K. In the case of the fully-filled La_0.25Yb_0.75Fe₃CoSb₁₂ [20], the minimum lattice thermal conductivity was reported to be 0.71 Wm^-1K^-1 at 723 K. In this study, the lattice thermal conductivity slightly increased as a result of partial double filling. Enhanced phonon scattering was expected by the double filling of La and Yb to reduce the lattice thermal conductivity. However, the enhancement of phonon scattering was not significant owing to the similar atomic masses and ionic radii of La and Yb, and the lattice thermal conductivity slightly increased over the fully-filled specimens.

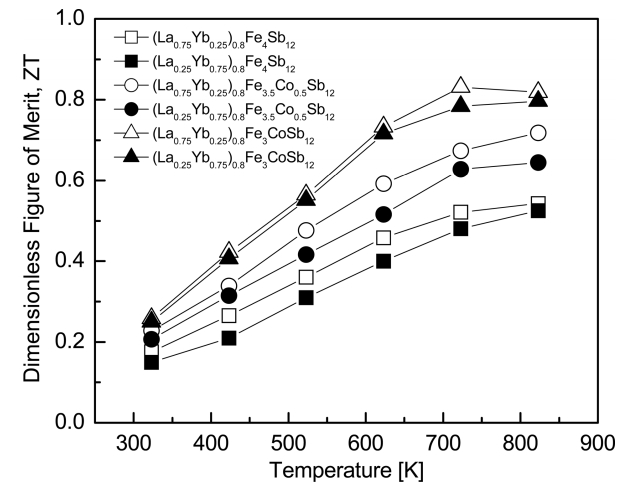
Figure 7 presents the temperature dependence of the ZT for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂. As the temperature increased, the ZT values increased and reached maximum values at temperatures between 723 and 823 K. (La_0.75Yb_0.25)_0.8Fe₃CoSb₁₂ exhibited ZT_max = 0.83 at 723 K owing to a higher power factor and a lower thermal conductivity. This value was higher than ZT_max = 0.64 at 723 K for the fully-filled La_0.75Yb_0.25Fe₃CoSb₁₂ [20]. Park et al. [23] reported ZT_max = 0.56 at 823 K for single filled LaFe₄Sb₁₂ and Park et al. [24] further obtained ZT_max = 0.59 at 823 K for single filled YbFe₄Sb₁₂. In our previous studies on the La/Pr- and Ce/Yb-partially-double-filled skutterudites, ZT_max = 0.79 was obtained at 723 K for (La_0.25Pr_0.75)_0.8Fe_3.5Co_0.5Sb₁₂ [18] and ZT_max = 0.66 was achieved at 823 K for (Ce0.25Yb_0.75)_0.8Fe_3.5Co_0.5Sb₁₂ [19]. However, Zhou et al. [25] reported high ZT_max = 0.99 at 700 K for La_0.60Yb_0.25Fe_2.7Co_1.3Sb₁₂. Therefore, in this study, partial double filling of La/Yb and charge compensation of Co were effective for the improvement of thermoelectric performance, and further improvement is expected through precise control of the filling ratio and substitution.

Fig. 7.

Temperature dependence of the ZT for (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂.

4. CONCLUSION

La/Yb-partially-double-filled and Co-substituted (La_1−zYb_z)_0.8Fe_4−xCo_xSb₁₂ skutterudites were synthesized by encapsulated melting and hot pressing processes. A small quantity of the marcasite was detected as a secondary phase along with the skutterudite phase. However, the marcasite phase formation was suppressed by Co substitution. As La filling and Co substitution increased, the Seebeck coefficient increased while the electrical conductivity decreased. The thermal conductivity significantly decreased with increasing Co substitution, and was further slightly lowered with increasing La filling. Compared to the La/Yb-fully-filled skutterudites, the thermoelectric performance was improved because of a higher Seebeck coefficient and a lower thermal conductivity. (La_0.75Yb_0.25)_0.8Fe₃CoSb₁₂ showed a maximum ZT of 0.83 at 723 K. Partial double filling of La/Yb and charge compensation of Co improved the thermoelectric performance, and further enhancement is expected through precise composition design.

Article information Continued