랜덤 트리 성장을 이용한 소성 경화 모델 개발방법 및 새로운 모델 제안
Development of a Novel Plastic Hardening Model Based on Random Tree Growth Method
Article information
Trans Abstract
The flow functions for plastic deformation have been developed to describe the plastic behavior of sheet metals. In order to explain the plastic behavior of material in metal forming processes via finite element analyses, two basic input functions should be applied. One is the yield function that determines the yielding behavior. The other is flow function to describe the hardening property of sheet metal. To describe the hardening properties of sheet materials under quasi-static tension condition in a wide range of plastic straining, various different equations are known such as classical Swift, Voce, Holloman, combined Swift-Voce, and recently proposed Kim-Tuan equations, etc. Those hardening equations are based on metallurgical or phenomenological investigations, and however the application of each equation has some limitation. In this study, the random growth of the binary tree method is introduced to develop the reliable hardening equations of various sheet metals (i.e. DP980, Pure Ti, AA5052-O, STS304, Ti-Gr2, and Mg-AZ31B) with no knowledge of existing hardening equation types. To evaluate the proposed method, the proposed equations developed by new approach are compared with the Voce, Swift, and Kim-Tuan hardening equations for stress-strain curve and the plastic instability point. Consequently, the proposed approach was proven to be very efficient to find the reliable and accurate hardening equation for any kind of materials.
1. 서 론
프레스 가공공정과 같은 재료의 소성변형 공정에 대한 유한요소해석 기술은 제품 개발단계에서 많은 시행오차 및 시간을 합리적으로 줄여주는 중요한 기법으로 자리잡았다. 그러나, 유한요소해석을 이용하여 재료의 소성가공공정에 대한 정확한 결과를 얻기 위해서는 유한요소해석 기법의 선정, 유한요소모델링, 경계조건 및 재료의 기계적 물성과 소성변형거동을 정확히 모사하는 재료 모델등이 필수적이다.
재료의 소성변형거동을 정확히 예측하기 위해서는 항복 조건과 재료의 경화모델의 선정이 필수적으로 고려되어야 한다 [1,2,3]. 항복조건을 구성하기 위한 첫째는 소성거동을 결정하는 항복함수의 선정이다. 항복함수는 다양한 하중을 받는 재료가 탄성영역 혹은 소성영역에 있는지를 결정하고 소성거동의 양상을 결정하는 수식이다 [4,5]. 둘째는 재료의 소성변형에서의 소성 경화 특성을 잘 표현하는 가공경화식이다. 가공경화식은 재료가 하중을 받을 때, 소성변형률 크기에 따라 응력이 점진적으로 증가하는 재료의 가공경화 특성을 나타낸다.
본 연구에서는 랜덤 트리 성장법을 소성가공분야에 적용하는 시작 단계로 소성 경화 모델 개발에 초점을 맞춰 연구를 진행하였다. 유한요소해석에서 가공경화식의 중요한 역할 중 하나는 제품을 성형할 때, 재료의 경화특성을 기술하는 것과 또한 가공 툴이 받는 반력의 예측이다. Fukumasu 등[6]은 AA3104 재료를 이용한 원형 컵드로잉 해석에 경화식이 미치는 영향을 평가하였다. 다양한 경화식은 성형을 위한 펀치의 반력 및 귀 발생에서 명확한 차이를 나타냄을 보였다. 여기서 응력을 과대평가하는 경화식은 펀치반력 또한 과대 평가한다는 것을 보였다. Pham 등[7]은 경화식이 성형한계도 예측에 미치는 영향을 평가하였고, 넥킹 후 소성변형거동의 과대평가는 성형한계도도 과대 평가한다는 것을 보였다. Kim 등[8]은 순 티타늄 판재의 사각굽힘 실험을 이용하여 경화식이 스프링 백 해석에 미치는 영향을 평가하였다. 변형률에 따른 응력을 정확히 예측하는 경화식은 순 티타늄 판재의 스프링백 해석에서의 정확성 또한 향상시킨다고 보고하였다. 또한 유한요소해석에서 적절한 경화식의 채용은 해석 정밀도 향상에 기여한다고 알려져있다 [9,10,11].
기존 연구에서 널리 사용되는 변형률 경화 모델로는 Swift모델[12]과 Voce모델[13]이 있다. 이 두 모델은 적은 파라미터의 개수로 인해 다양한 재료에 있어서 정확성에 명확한 한계를 가진다 [14]. 따라서 최근에 위 두 모델을 조합하여 다양한 가공경화 특성을 기술할 수 있는 Kim-Tuan모델[7,8]이 개발되었다. 이들의 일반적 형태는 다음과 같다.
여기서 σ0와 ε0는 재료의 초기 항복점에서의 응력과 변형률이며, 나머지 매개변수들 (A,b,K,n,T,m,c)은 최적화 알고리즘을 통해 구할 수 있다.
응력-변형률 관계를 더 정확하게 표현하는 관계식을 개발하는 데에는 파라미터 수와 이에 따라 증가하는 기하급수적인 경우의 수를 고려해야하기 때문에 유의미한 식을 얻기까지는 많은 시간과 노력을 요한다. 그 시도 중 하나로, 일부 재료에서 유효하다고 여겨지는 기존의 식을 변형하거나 새로운 항을 추가하는 등의 방법을 도입하고 있다. 예로, Voce모델과 Swift모델의 선형결합이 있다 [7]. 이와 같은 노력에도 불구하고, 여러 재료의 경화거동을 만족하는 식을 찾는데는 많은 수고가 요구되며, 또한 변태를 수반하는 티타늄 합금과 같은 경우나 고온과 고속에서의 재료 인장거동[15]을 기존의 식들로 표현하는 것에 한계가 있다. 여러 재료에 맞는 식을 개발하기 위해 파라미터의 수를 추가하여 식의 정보량을 늘리면 더 많은 유동양상을 가지게 되지만 파라미터의 값을 찾는 난이도와 식의 복잡도가 증가한다는 단점이 있다. 본 연구에서는 다양한 형태의 변수 항 및 연산자의 조합을 컴퓨터 연산으로 얻어 기하급수적 경우의 수 중에서 적절한 모델을 찾는 것을 목표로 한다. 이를 위해 식을 표현하는 방식인 이진 트리(binary tree)를 랜덤으로 생성하는 방법을 고안하였으며, 생성된 식을 주어진 재료의 응력-변형률 곡선에 피팅(fitting)하여 적절한 모델을 분류하여 제안하였다. 또한 제안한 모델의 신뢰성을 확인하기 위하여 6가지 재료에 대해 기존식들과 비교하였다.
2. 실험방법
2.1. 이진 트리를 이용한 모델의 개발 방법
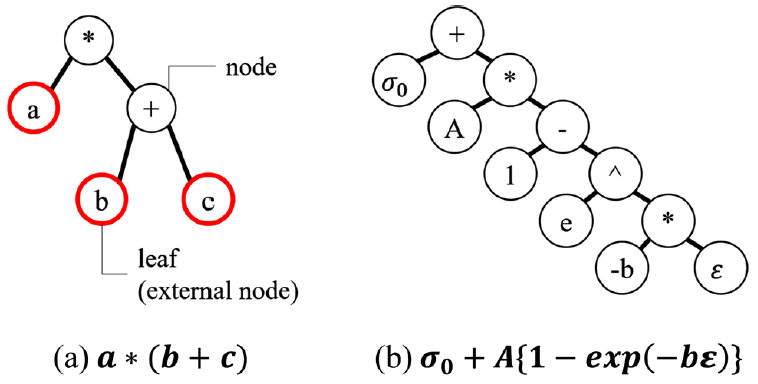
컴퓨터 과학에서 수식을 표현하기 위해 사용되는 자료구조 중 하나로 이진 트리가 있다. 이진 트리는 노드(node)로 구성되며 각각의 노드는 좌, 우로 두 개의 자식 노드(child node)를 갖는다. 말단 노드(external node)를 잎(leaf) 이라 한다. 이진 트리를 이용한 수식의 표현을 위해, 말단 노드에는 변수와 상수 및 매개변수를, 그 외의 노드에는 연산자를 부여할 수 있으며, 연산자 노드의 경우는 좌측의 자식 노드와 우측의 자식 노드의 연산을 의미한다. 단항 연산자의 경우 한 개의 자식 노드를 가지며, 규칙성을 위해 본 연구에서는 우측 자식 노드 만을 가지도록 정의하였다.
또한 파라미터, 상수에 대해 본 연구에서는 파라미터는 c1과 같이 최적화에 의해 값을 찾을 수 있는 요소로, 변수는 ε과 같이 데이터를 대입가능한 요소, 상수는 1, e (자연상수)와 같이 그 값이 정해져 있는 요소로 칭하도록 한다.
그림 1(a)와 (b)는 a*(b+c)와 Voce식을 이진 트리 형식으로 나타낸 예이다.
Examples of binary tree.
2.1.1. 이진 트리의 랜덤 성장 방법
수식 표현에 이용되는 이진 트리는 완전 이진트리(complete binary tree)가 아니기 때문에 성장시에 자식 노드의 결정 또한 랜덤하게 결정된다.
랜덤 트리의 성장 시 현재 말단 노드들 중 한 노드를 선택하여 성장하게 된다. 이 때 이항 연산자를 노드의 연산자로 채택할 경우 전체 말단 노드의 수는 1개 증가하게 되며, 단항 연산자를 채택할 경우 말단 노드의 수는 그대로 유지된다. 따라서 이항 연산자를 채택한 횟수가 곧 말단 노드의 수가 된다.
트리가 성장하여 말단 노드의 수가 파라미터, 변수와 상수의 수의 합과 같아지면 성장을 멈추고 말단 노드에 변수와 상수를 대입한다. 파라미터의 경우 순서가 바뀌어도 결과에 영향을 미치지 않기 때문에 순서대로 대입한다.
2.1.2. 모델의 생성 및 후보군 선정 방식
생성된 트리를 중위순회 (inorder traversal)방식으로 평가하여 프로그래밍 언어에서 해석할 수 있는 함수 형태로 변환한다. 이를 여러 재료의 응력-변형률 곡선에 피팅하여 파라미터의 값을 찾고, 식의 정량적 평가를 위하여 MSE (mean square error)를 구한다.
또한 여러 재료에 대해 피팅을 수행하므로 각 모델에 대해 여러 재료들의 MSE 평균을 사용한다. MSE 평균 외에 RMSE (root mean square error)의 평균값을 사용하더라도 기준의 특성이 조금 바뀌기는 하나, 오차가 적은 모델을 선택한다는 점에서 큰 차이는 없다.
MSE 평균의 값이 임의의 기준보다 낮을 경우 검토할 모델에 추가하여 모델의 적합성을 평가하게 된다. 상기의 과정은 컴퓨터 메모리 자원이 허락하는 한도 내에서 무한히 반복될 수 있으며, MSE 평균 값과 함수 형태의 비교를 통해 서로 중복되는 모델은 검토에서 배제한다. 그림 2에 랜덤 트리를 이용한 경화식 개발의 순서도 (flow chart)를 나타내었다.
Flow chart to develop the hardening model.
본 연구에서는 AA5052, DP980, Pure Ti, Mg-AZ31B, STS304, Ti-Gr2 총 6가지의 재료에 대하여 피팅을 수행하였다.
Pure Ti [16], DP980, AA5052-O [17]의 데이터는 선행 연구로부터 얻어진 결과를, Mg-AZ31B, Ti-Gr2, STS304의 데이터는 KS B-13호 시험편을 이용하여 변형률 속도 0.001/s로 시험한 결과를 사용하였다.
3. 실험결과 및 고찰
3.1. 모델 생성 결과 및 분류
3.1.1. 수행 조건의 설정
수행조건을 설정하기 위해서는 파라미터와 변수의 개수 및 상수의 구성을 설정해야 한다. 이 역시 랜덤 과정을 통해 실행시간 (runtime)중에 결정할 수 있지만 그 경우의 수가 한정적이므로 본 연구에서는 통제가능한 요소로 설정하였다.
연산자는 덧셈(+), 뺄셈(-), 곱셈(*), 나눗셈(/), 제곱(^) 및 자연로그(ln)로 구성하였고, 이들의 각 노드당 확률적 빈도는 같게 설정하였다. 따라서 각 연산자가 선택될 확률은 각각 1/6이다. 이 외에도 다양한 형태의 함수를 포함시키는 것이 가능하나 식의 복잡성, 미분의 복잡성 및 기존 식의 형태를 고려하여 우선적으로 상기의 연산자만을 포함하였다. 연구자의 판단에 따라 더 많은 초월함수들을 포함시키는 것 또한 가능하다.
상수는 개별항을 구성한다는 것에 의의가 있으므로 2, 3, 4와 같은 상수는 구성에서 제외하였으며, 1과 자연상수 e로 구성하였다. 변수와 파라미터 및 상수들은 구성조건에 속해 있다면 항상 식의 구성요소에 포함되어야 한다. 다만, 자연로그의 항에 1이 들어가는(즉, ln(1) = 0) 등의 상황에서 트리상으로는 공식에 포함되었으나 전개해보면 성분에 없는 상황이 발생할 수 있다. 또한 c1 + c2와 같이 상수끼리 연산이 되는 무의미한 상황이 발생하는 경우도 빈번하다. 본 연구에서는 이와 같은 상황에서 이를 하나의 상수로 취급하여 파라미터의 값을 다시 구하였다. 따라서, 결과로 나오는 식은 설정한 상수의 개수보다 적을 가능성이 있다.
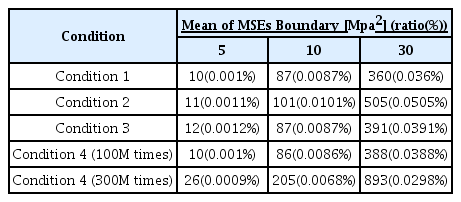
일반적인 환경의 컴퓨터에서 그림 2의 과정을 수행하였으며 상수와 파라미터, 변수의 구성에 따라 가능한 식의 표현 범위가 달라지기 때문에 여러 조건에서 수행하였다. 대표적인 수행 조건과 이에 따라 생성된 특정 MSE경계값 이하의 모델 개수는 각각 표 1과 표 2에 나타내었다.
Execution condition.
Number of models that Mean of MSEs is under boundaries.
평균적으로, 100만회까지의 조건에서 본 연구에서 유의미한 의미를 얻을 수 있다고 여겨지는 5 Mpa2 이하의 MSE 평균을 가질 확률은 0.001%정도인 것으로 파악된다. 5~10 MPa2이하의 MSE평균을 갖는 모델은 값이 매우 미미하므로 보통 원본데이터 영역에서 육안상으로는 오차를 구분하기 어렵다.
3.1.2. 생성된 모델의 분류
생성된 모델들은 오직 MSE 평균을 통해 평가되었기 때문에 적절한 모델을 연구자의 주관으로 분리할 필요가 있다. 본 연구에서는 다음 5가지의 기준으로 적절한 모델들을 분류하였다.
(1) 주어진 범위 내에서 단조 증가한다. (미분식이 항상 양수이다)
(2) 모든 범위에서 데이터와의 오차가 작다.
(3) 식의 복잡도가 낮다.
(4) 미분 식의 복잡도가 낮다.
(5) 최대 인장 강도 지점의 예측이 정확하다.
위 기준들은 적절한 알고리즘을 사용해 자동화할 수 있지만 대상 모델의 수가 많지 않기 때문에 연구자에 의해 수행되었다.
판재 재료의 소성불안정과 관련한 최대 인장 강도 지점(Maximum Tensile Force Point, MTFP)의 정확도 기준이 되는 오차는 변형률과 응력에 대해 고려해야 하므로 상대 오차 공간에서의 유클리디안 거리 (Euclidean distance)를 이용하였다.
σexp : 최대 인장 강도 지점의 응력 실험값
σpre : 최대 인장 강도 지점의 응력 예측값
εexp : 모델의 최대 인장 강도 지점의 응력 실험값
εpre : 모델의 최대 인장 강도 지점의 응력 예측값
3.2. 생성된 소성 경화 모델의 제안
3.2.1. 생성된 소성 경화 모델의 예시
본 연구에서 제안한 방식에 의해 생성된 소성 경화 모델들은 주어진 데이터에 대해 매우 낮은 오차를 가지지만 3.1.2장에서 제안한 기준들에 부합하는 모델의 비율은 매우 낮았다.
MSE 평균이 5 MPa2이하인 모델들 중 단조 증가하는 모델만을 선정한 결과는 다음과 같다.
여기서 ci(i:1~5)는 피팅 파라미터이다. model-3과 model-4는 미분 형태가 매우 복잡하므로 실용가치가 떨어지는 것을 판단하였고, model-1과 model-2는 비교적 간단한 미분형태를 가지므로 적합한 모델로 판단하였다. model-2에서 ε항(변형률 항)은 다른 항에 비해서 매우 작은 값을 가지기 때문에 생략할 수 있으며, 피팅 결과 c1은 초기 항복응력 σ0와 유사한 값을 가지기 때문에 대체하여 파라미터가 4개인 식으로 사용하여도 오차의 차이가 크지 않으며 초기 항복점을 정확하게 지나는 모델을 얻을 수 있다.
3.2.2. 생성된 모델 중 분류된 모델의 제안
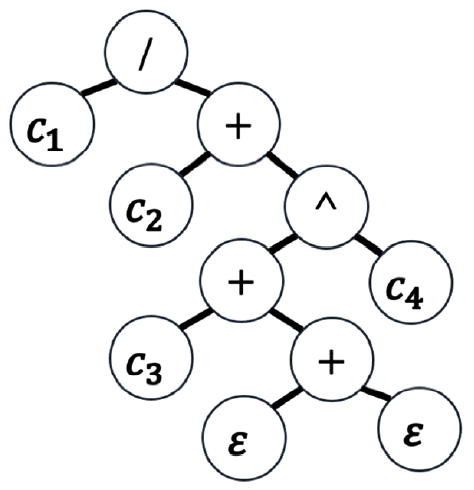
본 연구에서 생성된 모델 중 연구자에 의해 분류되어 유의미한 결과를 갖는다고 생각되는 모델인 model-1을 소성경화 모델로 제안한다 (이하 Proposed로 표기한다.)
식 (10a)와 같이 ε항은 본래 계수가 2였으나 계수가 1인 것과 무시할 수 있을 정도의 차이를 가져, 식 (10b)와 같이 단순한 형태인 계수 1을 사용하였다. 제안한 모델에서 c2에 0을 대입하고 c4를 −c4로 대체하면 Swift 모델이 얻어진다는 것을 알 수 있다.
그림 3에 식 (10a)을 이진트리 형식으로 나타내었다.
Binary tree representation of plastic hardening equation (10a).
3.2.3. 제안된 소성 경화 모델의 응력-변형률 관계 묘사
총 6가지의 선택된 재료에 대한 응력-변형률 관계를 Swift, Voce, Kim-Tuan 모델에 각각 대입하여 커브 피팅하였고 그 중 주요 3가지 재료에 대한 그래프를 그림 4에 나타내었다. 나머지 3가지 재료는 본문의 페이지 수를 고려하여 부록 (그림 A.1)에 정리하였다. 개발한 식 (10a)이 가장 낮은 평균 MSE오차를 나타냄을 확인하였다.
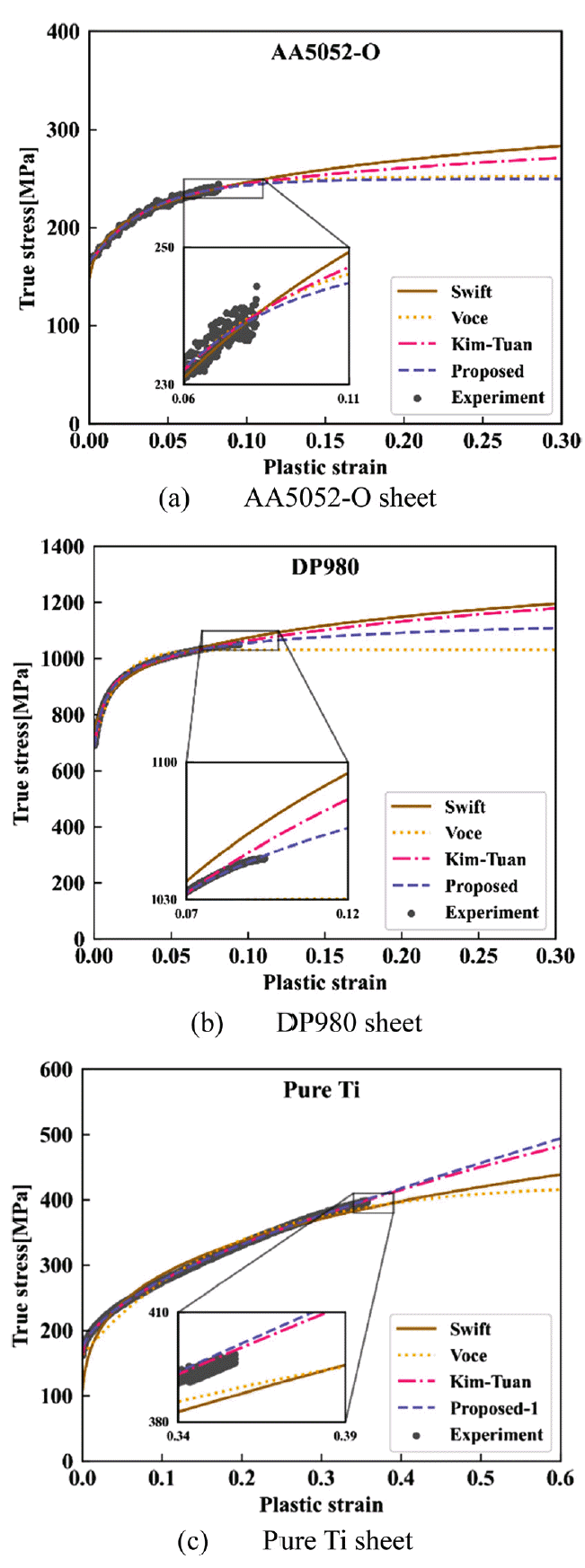
True stress-strain curves from four hardening functions with experiment for three principal materials.
AA5052-O의 경우 Kim-Tuan식은 Swift식과 Voce식 사이의 함숫값을 가지는 반면 제안한 식은 Voce식과 거의 일치하였다. DP980의 경우 제안한 식은 최대 하중 지점 이후로 Kim-Tuan식보다 낮은 함숫값을 가졌다. Pure Ti에서는 제안한 식과 Kim-Tuan식이 거의 같은 양상을 보이며 최대 하중 지점 이후에서는 제안한 식이 조금 더 높게 예측되었다.
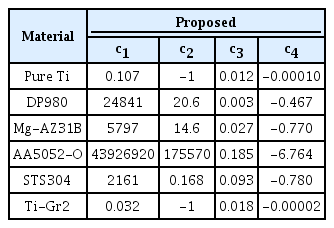
피팅 결과 Pure Ti를 제외한 재료에 대해서 제안한커브 피팅으로 얻어진 파라미터 값들은 표 3과 표 4에 각각 나타냈다. DP980, Mg-AZ31B, AA5052-O, STS304의 경우 c2가 양수이고 c4의 절대값이 비교적 크기 때문에 (c3+ ε)c4의 항이 0으로 수렴한다. 따라서 함숫값은 c1/c2로 수렴하는 것을 알 수 있다. 또한 c4의 절대값이 가장 큰 AA5052-O의 경우 Voce식과 비슷한 유동을 보이는 것을 알 수 있다. 반대로 c2의 값이 -1인 Pure Ti와 Ti-Gr2의 경우 c3 + ε 이 1이 되어 (c3 + ε)c4 항 또한 1이 될 때 분모가 0이 되어 함숫값이 무한대로 발산한다. 따라서 제안된 식은 수렴과 발산의 형태를 모두 가질 수 있다.
Curve fitting results of four hardening models for studied materials.
Curve fitting results of Proposed models for studied materials.
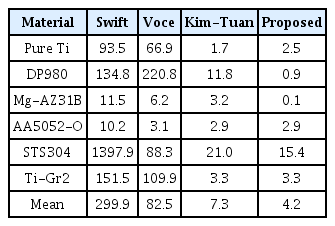
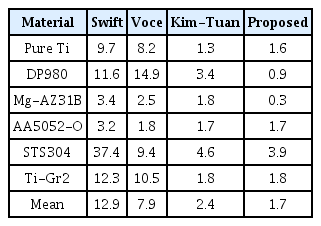
MSE 오차를 표 5에 6가지 재료와 4가지 모델에 대해 구하였다. 또한, 오차의 단위가 MPa2 이기 때문에 더 직관적인 구분을 위한 RMSE오차를 표 5에 나타내었다.
Mean Square Error [MPa2] estimation of four hardening models for studied materials.
3.2.4. 제안된 모델의 최대 인장 강도 지점 예측
제안된 모델의 최대 인장 강도 지점 (ε*, σ*)를 통해 인장 하에서 소재에 불안정한 넥킹(necking)이 발생하는 지점을 판단할 수 있다. 이 위치는 유동곡선의 함수 값과 미분 값에 동시에 영향을 받기 때문에 함수의 정확도를 나타내는 척도가 될 수 있다.
Swift의 확산넥 이론에 따라 판재의 최대 인장응력의 상태는 다음과 같이 표현된다.
이를 소성변형 중의 체적일정 조건 하에서 에 대해서 정리하면 다음과 같다.
제안한 식 (10a)의 미분형태는 다음과 같다.
이 중 식 (10a)에 따라 c2 + (c3+ ε)c4 = c1/σ와 같이 표현이 가능하기 때문에 식 (13)은 다음과 같이 나타낼 수 있다.
식 (12)에 따라 제안한 식의 최대응력상태는 다음과 같이 나타낼 수 있다.
위 식의 양변을 정리하여 MTFP, (ε*,σ*)을 대입하면
와 같은 관계식을 얻을 수 있다.
AA5052-O와 같은 판재에서 제안된 식은 미분 값이 빠르게 0으로 수렴하는 성질이 있기 때문에 수치해석 방법에 따라 MTFP의 해를 정확히 얻지 못할 수 있다. 이와같은 경우, 식 (16)은 수치해석적으로 얻어진 MTFP 해를 검증하는데 이용할 수 있다.
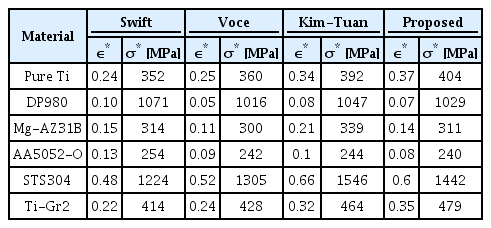
표 3과 표 4에서 얻어진 파라미터 값으로 4가지 모델에 대한 MTFP지점을 그림 5에 나타내었다. 나머지 3가지 재료는 본문의 페이지 수를 고려하여 부록(그림 A.2)에 정리하였다.
True stress-strain curves and MTFP obtained from four hardening functions with experiment for three principal materials.
제안된 모델은 AA5052-O 재료에서는 Voce 모델과 같은 양상으로 미분값이 0으로 수렴하며, MTFP의 예측에 있어서 가장 정확함을 확인할 수 있었다. DP980재료에서는 Swift식의 MTFP 오차가 가장 작았으며 Kim-Tuan식의 경우 MTFP 지점에서의 응력 오차가 가장 작은 것을 확인할 수 있었다. Pure Ti에서는 본 연구에서 제안한 식의 MTFP 오차가 가장 작았으며 Kim-Tuan식의 MTFP 지점에서의 응력 오차가 가장 작았다. 결과적으로 6가지 재료에 대해 MTFP 오차를 평균을 구했을 때 제안한 식의 MTFP 오차가 다른 식의 절반 이하로 작았다.
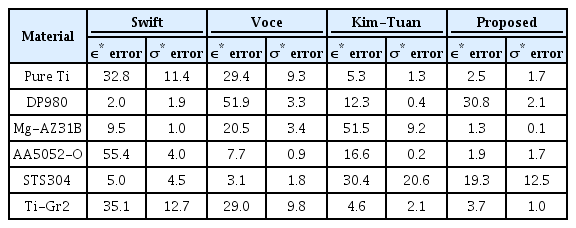
MTFP의 자세한 값을 표 7에, 표 8의 실험 MTFP값에 대한 변형률 상대오차와 응력 상대오차를 표 9에, 식 (5)에서 제안한 MTFP오차를 표 10에 표시하였다.
MTFP estimation of four hardening models for studied materials.
experimental MTFP value for six studied materials.
MTFP relative error (%) estimation of four hardening models for studied materials.
Mean of MTFP error (%) estimation of four hardening models for studied materials defined by equation(5).
결과적으로 표 9에 따라 제안된 모델은 STS304 판재를 제외하면 MTFP의 응력 성분 상대오차가 3%미만의 양상을 보이는 것을 확인하였다.
3.2.5. 제안된 모델의 소성 변형 안정성 보장
표 4에서 얻어진 결과에 따르면 6가지 재료 모두에서 c1과 c3는 양수, c4는 음수, c2는 양수 값과 음수 값 모두를 가지는 것을 알 수 있다. 식 (15)에서 ε항은 항상 양수인 것을 알고 있으므로 주어진 파라미터 범위에서 δσ/δε는 항상 양수라는 것을 알 수 있다. 이는 제안된 모델의 파라미터 c2를 제외하고 양수, 음수 범위에서 제한함으로써 미분값을 양수로 유지하여 단조증가를 보임으로써 드러커 (Drucker)의 소성 변형 안정성 [18]을 보장할 수 있다는 의미이다.
3.2.6. 제안된 모델의 초기 항복점 예측
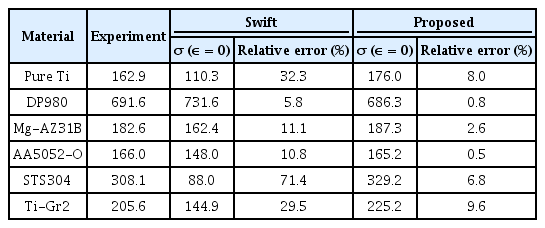
초기 응력값은 경화식에 ε항에 0을 대입하여 얻을 수 있다. Voce식과 Kim-Tuan식은 이미 초기 항복응력값을 식에 포함하고 있으므로 오차는 0%이다. 따라서 Swift식과 제안한 식을 비교하였다.
실험값과의 상대오차(%)는 표 11과 같으며 제안된 식은 초기 항복 응력값이 없음에도 DP980, Mg-AZ31B, AA5052-O에서는 3%미만의 오차를 보여주었고, 나머지 Pure Ti, STS304, Ti-Gr2에 대해서도 30%이상 차이나는 Swift식과 대비하여 10% 미만의 상대오차를 보였다.
Relative error of initial yield stress of two hardening models for studied materials.
3.2.7. 초기 항복점을 지나는 제안된 모델의 변형된 형태
제안된 모델(식 (10b))는 초기 항복점에 대한 정보가 없기 때문에 일정수준의 오차를 가진다.
식 (10b)에 초기 항복점으로 (0, σ0)를 대입하면 파라미터를 3개로 감소시킬 수 있으며 제안한 소성경화식이 초기 항복점을 지나게 할 수 있다.
즉, 식 (10b)에 (0, σ0)를 대입하면
c1에 대해서 정리하여 다시 식 (10b)에 대입하면
를 얻을 수 있다.
c1이 제거되었으므로 이를 다시 정리하면 다음과 같이 나타내진다.
식 (19)를 이용하면 제안된 모델이 이미 초기 항복점 근처를 지나기 때문에 피팅 시에 기존의 파라미터 값과 비교하면 미미한 차이를 보인다. 또한 파라미터의 개수가 3개로 줄어들었으므로 피팅의 난이도가 비교적 낮아진다는 것을 알 수 있다.
수정된 제안식 (식 (19))는 RMSE오차가 2.4 MPa로, 기존에 제안된 식 (식 (10b))의 1.7 MPa에 비해 소폭 상승하였음을 확인할 수 있다. 또한 MTFP오차의 평균은 14.9%로 제안된 식의 10.7%보다 4.2%P상승하였음을 알 수 있다. 따라서 식의 활용목적에 따라 초기 항복점을 정확히 지나는 변형 형태를 사용하거나 MTFP오차가 비교적 작은 모델을 선택하여 사용할 수 있다.
4. 결 론
4.1. 제안된 모델의 실효성을 통한 새로운 경화모델 방법의 가능성 고찰
본 연구에서는 기존의 소성경화식에 대한 지식이 없는 상태에서 알고리즘의 주어진 방식에 따라 방정식을 완전 랜덤으로 생성 및 피팅하여 제안된 모델과 같이 소성경화식을 확률적으로 찾아낼 수 있다는 점을 확인하였다.
표 6과 표 8에서 제안된 식의 결과는 기존 식들과 대비하여 좋은 결과를 보여주었으며 이는 본 연구가 제안하는 모델 개발 방식의 유효성을 보여준다.
Root Mean Square Error [MPa] estimation of four hardening models for studied materials.
본 연구에서는 오직 MSE만을 모델의 기준 조건으로 설정하고 나머지 분류작업은 연구자에 의해 수행되었으나, 적절한 알고리즘에 따라 나머지 또한 컴퓨터에 의해 자동화될 수 있다. 일례로 본 연구에서는 제안된 식의 개발 이후, 자동으로 식을 미분하여 MTFP를 찾은 후 오차를 계산하고 경계값 아래의 모델을 분류하는 과정까지 자동화를 완료하였고, 이 연구에 대해서는 후속 논문에서 발표할 예정이다.
본 연구에서 제안한 기준 외에 대변형 소성 유동의 예측 등도 연구자의 필요에 따라 얼마든지 알고리즘에 포함시킬 수 있다. 자원이 허락하는 한도 내에서 까다로운 조건을 만족시키는 모델을 적은 수고로 찾을 수 있는 것이 본 연구가 제안하는 모델 개발 방식의 최대 효용이라 할 수 있다.
또한 병렬 프로그래밍 등 현존하는 하드웨어 기술을 이용함으로써 제안한 방식의 성능적 향상을 기대할 수 있다.
4.2. 제안된 경화 모델 개발 방식의 개선방향
본 연구에서 제안한 모델 개발 방식은 초기 설정과 피팅 및 분류 외의 모든 과정이 완전 랜덤으로 이루어지기 때문에 중복 등의 문제로 인해 시간의 낭비가 주요 문제점이다. 일반적인 6~16코어 컴퓨터에서 시간당 10000~30000개 가량의 모델을 검토하는 것을 확인할 수 있었다. (100만개 기준 대략 30시간) 시간당 검토가능한 모델의 수를 올리는 것은 성능향상의 문제이므로 본 연구에서는 같은 수의 모델을 검토하였을 때 더 많은 유효한 모델을 얻기 위한 기초적 방법을 아래와 같이 제안한다.
4.2.1. 연산자와 초기설정의 확률 가중치 부여
본 연구에서는 6개의 연산자가 각 노드에 포함될 확률이 각각 1/6로 같도록 하였으나 제곱, 자연로그와 같은 연산자는 model-3 및 model-4와 같이 미분형태가 매우 복잡할 확률이 높다. 따라서 이와 같은 연산자들의 확률빈도를 줄이는 것을 제안한다. 또한 표 2에서 보았듯이 자연로그를 전혀 사용하지 않은 실행조건의 경우 MSE가 기준 이하인 모델의 빈도가 타 조건에 비해 높은 현상은 미분 복잡도의 문제만이 아닌 조건을 만족시키는 모델의 빈도 또한 높일 수 있다는 가능성을 보여준다.
연산자 뿐 아니라 상수, 변수, 파라미터의 구성에 따라서도 유효한 모델의 빈도는 달라질 것이므로 이에 대한 통계적 접근은 제안한 개발방식의 실효성을 높여줄 수 있다.
Acknowledgements
이 논문은 2019 대한민국 교육부와 한국연구재단의 지원을 받아 수행된 연구임 (NRF-2019R1A2C1011224).
References
Appendices
APPENDIX A Fig. A.1. True stress-strain curves from four hardening functions with experiment for three extra materials.
Fig. A.2. True stress-strain curves and MTFP obtained from four hardening functions with experiment for three extra materials.
