Transition to n-type Thermoelectric Conduction in Ni-doped FeSe₂ Alloys

Article information

Abstract

1. INTRODUCTION

Thermoelectric materials have attracted considerable attention as sustainable energy technologies because they can convert a temperature gradient into an electrical potential. Thermoelectric performance is quantified as a dimensionless figure of merit (zT), where high zT values indicate high thermoelectric transfer efficiency. However, improving zT to achieve high thermoelectric performance is challenging. By definition, zT is σ·S²·T/κ_tot, where σ, S, κ_tot and T are the electrical conductivity, Seebeck coefficient, thermal conductivity, and absolute temperature, respectively. σ·S² is referred to as the power factor, and κ_tot = κ_elec + κ_latt, where κ_elec is the electronic thermal conductivity and κ_latt is the lattice thermal conductivity. Therefore, for a high zT, either the power factor (σ·S²) should be increased or the thermal conductivity (κ_tot) should be decreased [1-3].

To improve σ·S², it is necessary to consider the trade-off relationship between σ and S (i.e., S decreases as σ_increases), which leads to the determination of the enhanced power factor. In the case of κ_tot, studies have been conducted to reduce the κ_latt. In general, the reduction of κ_latt is achieved through structural properties such as two-dimensional layered structures or point-defect phonon scattering [4-6]. For Bi-Tebased materials, the two-dimensional layered structure has a Van der Waals gap in the out-of-plane direction; therefore, the thermal conductivity is low, but the electrical conductivity is high in the in-plane direction [7]. However, this structure only materializes in certain compounds despite exhibiting good anisotropy; therefore, point defects have been introduced in thermoelectric alloys via doping or solid solution method to increase phonon scattering [8,9].

Conventional chalcogenides including Bi₂Te₃ have been extensively studied as thermoelectric materials. Chalcogenides have semiconducting properties and exhibit high thermoelectric performance by reducing the thermal conductivity via nanostructuring. In particular, transition-metal dichalcogenides have good optical, electrical, magnetic, and transport properties. In addition, in certain transition metal compounds, the effective mass is sometimes large because of the partially filled electrons in the d and f orbitals, which can improve the power factor (σS² ∝ m^*3/2μ), where m^* is the effective mass and μ is the mobility [8-10].

To further enhance thermoelectric performance, both the nand p-type thermoelectric materials must have similar zT values. Studies have been conducted to improve the transport properties in p-type materials using mechanisms such as impurity doping, solid solution, and vacancy formation in chalcogenide compounds such as GeTe, Cu₂Se, Bi₂Te₃, SnSe, SnTe and Bi₂Te_2.7Se_0.3 [11-16]. Bi-Te based materials exhibit good thermoelectric performance (zT ≈ 1.8) at room temperature, and the thermoelectric performance of Al-doped Cu₂Se increased to zT ≈ 2.6 at a high temperature of 1029 K [12,13]. However, improving the thermoelectric performance of n-type materials requires additional investigation.

Recently, the thermoelectric properties of n-type thermoelectric materials have been improved using the structural properties of Zintl or skutterudites. For example, Ba_0.3In_0.3Co₄Sb₁₂, a skutterudite material, has a zT of approximately 1.8 at 850 K and Mg_3.02Y_0.02Sb_1.5Bi_0.5, a Zintltype material, has a zT of approximately 1.8 at 773 K, but poor thermoelectric performance at room temperature [17,18].

Fe-based chalcogenides have also been studied as thermoelectric materials [19-21]. Among Fe-based chalcogenides, FeSe₂ has good electrical transport properties with a carrier concentration of 10¹⁸-10¹⁹ cm^-3 [22]. In addition, FeSe₂ exhibits a bipolar effect in which the main carrier is inverted at high temperatures [19]. Therefore, obtaining a specific material by enhancing or changing these characteristics is possible.

Based on these conceptualizations, this study was conducted to investigate the electrical and thermoelectric properties of the transition-metal chalcogenide, FeSe₂ doped with Ni. The σ, S, Hall carrier concentration, and Hall mobility were measured and the m^* was calculated from the S and Hall carrier concentration.

2. EXPERIMENTAL

To synthesize the reference FeSe₂ and Ni-doped Fe_1-xNi_xSe₂ (x = 0.01, 0.05, 0.075, 0.1, and 0.125) samples, stoichiometric amounts of Fe, Se, and Ni powders were mixed. The samples were synthesized at 560 K for 72 h via a conventional solid-state reaction. High-purity Fe (99.9%, Alfa Aesar), Se (99.999%, KRTLab), and Ni (99.9%, Alfa Aesar) were loaded in a quartz tube (diameter = 15 mm), which was then vacuum sealed (~10^-3 Torr). The synthesized ingot was pulverized in a stainless steel container with stainless steel balls using a high-energy ball mill (SPEX 8000D, SPEX) for 5 min to obtain the powders. The bulk sample was fabricated under vacuum (~10^-5 Torr) by spark plasma sintering (SPS; SPS-1030, Sumitomo Coal Mining Co., Ltd., Tokyo, Japan) at 530°C for 14 min at 75 MPa.

The crystalline phase analysis of the samples was performed using X-ray diffraction (XRD, D8 Discover, Bruker) at 40 kV and 40 mA. The XRD patterns were recorded in the 2θ range of 20°-80° at a scan rate of 0.02° s^-1 using a Cu K_α source, and the lattice parameter was calculated based on the XRD patterns for each synthesized sample. The thermoelectric properties S and σ were simultaneously measured over a temperature range of 300-600 K in a direction parallel to the SPS pressing direction, using a thermoelectric property measurement instrument (ZEM-3, Advanced-Riko, Yokohama, Japan). The error margins for σ and S were less than 3% and 5%, respectively. Hall measurements were performed at room temperature in the same direction using the Van der Pauw method to determine carrier concentration (n_H) and mobility (μ_H). The κ_tot value of the sample was calculated using the theoretical density (ρ_s), heat capacity (Cp), and thermal diffusivity (λ) (κ_tot = ρ_s·Cp·λ). Further, ρ_S of FeSe₂ was 7.09 g/cm³ and Cp was measured using a differential scanning calorimeter (DSC8000, Perkin Elmer, Waltham, USA). The λ value was measured in the temperature range of 300-600 K along the pressing direction, using the laser flash method (LFA457, Netzsch, Selb, Germany). The error margin for λ was less than 7%. Accordingly, zT was evaluated based on data measured in the SPS pressing direction. The error margin for zT would be less than 15%.

3. RESULTS AND DISCUSSION

Figure 1(a) shows the XRD patterns of the synthesized Fe_1-xNi_xSe₂ (x = 0, 0.01, 0.05, 0.075, 0.1, 0.125, and 0.2) samples. From the XRD patterns, except for the doping level of x = 0.2, a single phase of FeSe₂ with a marcasite structure was confirmed without a Ni-related secondary phase. However, secondary phases including Fe2NiSe4 were observed in the x = 0.2 sample, which suggests that the Ni atoms were not well doped in the FeSe₂ alloy after doping with x = 0.2. Therefore, subsequent measurements were performed, except for the x = 0.2 sample. The lattice parameters a, b, and c are shown in Fig 1(b) and were calculated using the (111), (012), and (121) diffraction peaks. The lattice parameters increased systematically with increasing Ni doping levels. This is because the ionic radius of Ni²⁺ is 0.72 Å, which is larger than that of Fe³⁺ (0.65 Å) [23,24].

Fig. 1.

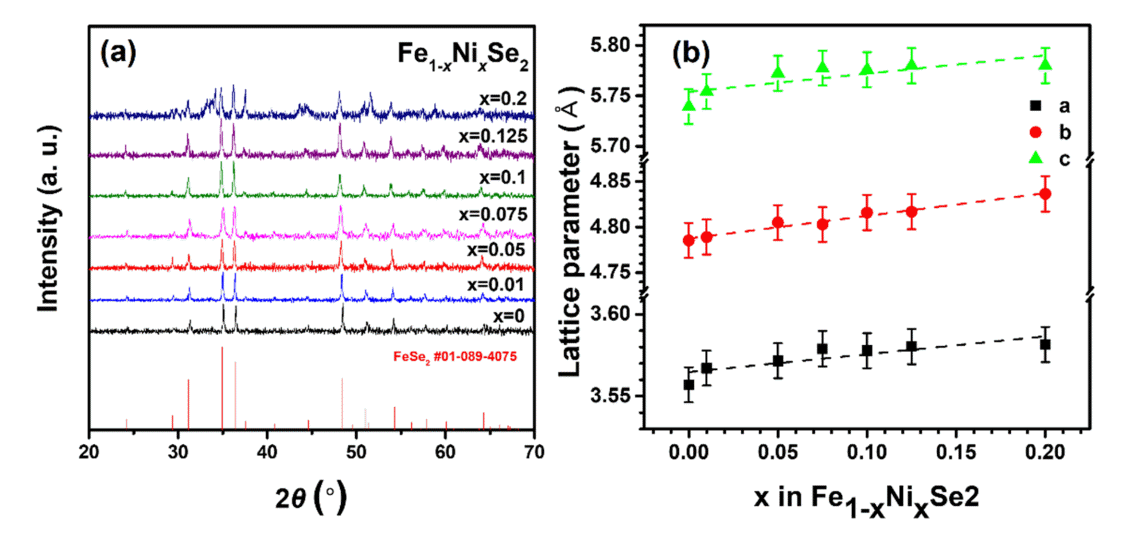
(a) XRD patterns, and (b) calculated lattice parameters for the Fe_1-xNi_xSe₂ (x = 0, 0.01, 0.05, 0.075, 0.1, 0.125 and 0.2) samples

Figure 2 shows the measured σ and S values at different temperatures and the calculated power factor. The σ values (Fig 2(a)-(d)) systematically increased from 8.52 (undoped) to 328.78 S/cm (x = 0.125) at 300 K, with increasing Ni doping level, by approximately 38.6 times. The S plot of the undoped FeSe₂ sample (Fig 2(b)) shows that a bipolar effect occurs, in which the main carrier is reversed between 400 and 450 K, but the Ni-doped samples had no bipolar effect and were converted to n-type semiconductors (Fig 2(e)).

Fig. 2.

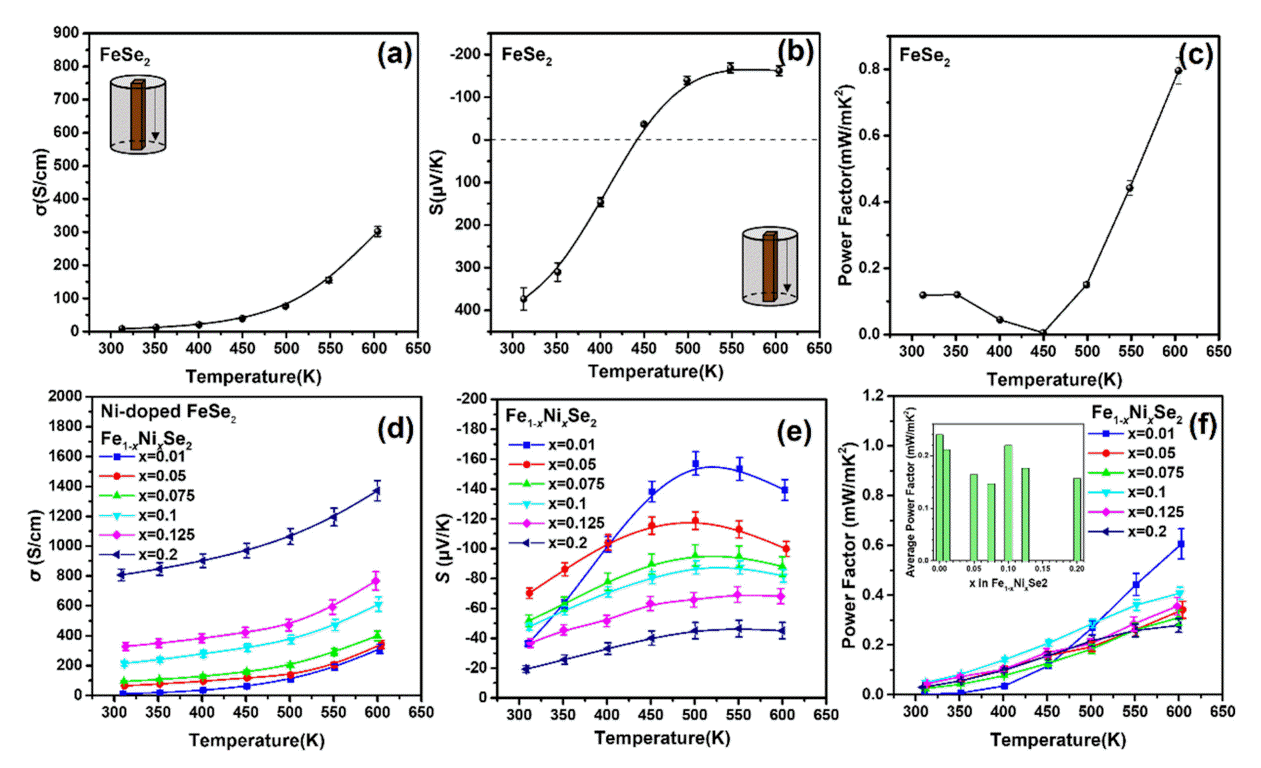
(a) Electrical conductivity, (b) Seebeck coefficient, and (c) Power factor as a function of temperature for the undoped FeSe₂ and (d) electrical conductivity, (e) Seebeck coefficient, and (f) power factor as a function of temperature of the Fe_1-xNi_xSe₂ (x = 0.01, 0.05, 0.075, 0.1, 0.125 and 0.2) samples.

In addition, the plot of the sample with a doping level x = 0.01 was abnormal; this phenomenon could be caused by the conversion to an n-type semiconductor. That is, it can be described as an intermediate composition converted to ntype. The S values of the Fe_1-xNi_xSe₂ samples systematically decreased from -70.31 to -36.71 μV/K at 300 K, from the doping level, x = 0.05 to x = 0.125 due to the trade-off relationship with σ. Consequently, due to the bipolar effect, the power factor of the undoped FeSe₂ (Fig 2(c)) showed the highest values of 0.120 and 0.796 mW/mK² at 300 K and 600 K, respectively.

In the case of the power factor of the Ni doped-FeSe₂ samples, at 300-500 K, the doping level of x = 0.1 showed a maximum value of 0.049-0.287 mW/mK², and the power factor of x = 0.01 became larger at subsequent temperatures. The average power factor values calculated over the entire temperature range are also shown in the inset of Fig 2(f). The average power factor had a maximum value at x = 0.1, except for undoped FeSe₂, which exhibited a bipolar effect.

Figures 3(a) and 3(b) show the logarithmic σ plotted against 1000/T and the calculated activation energy (E_a), respectively. Because E_a is proportional to the negative slope for σ_in Fig 3(a), it was calculated using the Arrhenius relationship, σ ∝ exp(-E_a/kT), where k is the Boltzmann constant; the E_a values are plotted for the 300-400 K and 400-600 K temperature ranges. The E_a values gradually decreased with increasing doping levels at all temperature ranges and had higher values at higher temperatures than at lower temperatures.

Fig. 3.

(a) Logarithmic electrical conductivity as a function of 1000/T. The slope is proportional to the activation energy. (b) Calculated activation energy, (c) Hall carrier concentration, (d) Hall mobility and (e) effective mass, as a function of x for the Fe_1-xNi_xSe₂ (x = 0, 0.01, 0.05, 0.075, 0.1, 0.125 and 0.2) samples. (f) S as a function of the measured carrier concentration (Pisarenko plot) at room temperature.

Figure 3(c) shows the Hall carrier concentration (n_H), where n_H is expressed as the hole concentration (n_h) for undoped FeSe₂ and the electron concentration (n_e) for n-type Ni-doped FeSe₂. The absolute n_H values of Fe_1-xNi_xSe₂ gradually increased from 1.44 × 10¹⁹ (x = 0) to 9.54 × 10²⁰ cm^-3 (x = 0.125), which suggests that the n_H values systematically increased with doping level. As shown in Fig 3(d), the μ_H values significantly decreased from 3.51 (x = 0) to 0.60 cm²/Vs (x = 0.01) at 300 K due to the significant increase in carrier concentration. However, for doping levels, x = 0.01 to x = 0.125, μ_H increased systematically at 300 K from 0.60 (x = 0.01) to 2.13 cm²/Vs (x = 0.125).

Figures 3(e) and 3(f) show the effective mass and log₁₀(n_H) as a function of S, at 300 K, for the Fe_1-xNi_xSe₂ samples. The solid line in Figure 3(f) was calculated using the following equations for n_H and S for different effective masses:

For all samples, the plots were inferred numerically using Equation (1), and the m_d^* values were maximum at x = 0.1 [25]. Further, as shown in Fig 2, the electrical conductivity almost doubled with an increase in doping level from x = 0.075 to x = 0.1; however, the Seebeck coefficient did not significantly increase. These results indicate that m_d^* was modified in favor of S at a doping level of x = 0.1.

Figure 4(a) and (b) show the plots of κ_tot and κ_latt, respectively. the plot of κ_elec is given in the inset of Fig 4(b), where κ_elec is calculated using the Wiedemann-Franz equation.

Fig. 4.

(a) Total thermal conductivity, (b) lattice thermal conductivity and inset of (b) is electronic thermal conductivity as a function of temperature, for the Fe_1-xNi_xSe₂ (x = 0, 0.01, 0.05, 0.075, 0.1, 0.125 and 0.2) samples.

where L denotes the Lorenz number. As shown in Fig 4(a), at 300 K, κ_tot systematically decreased from 6.81 to 4.29 W/mK, but at temperatures above 500 K, the trend changed because the slope of κ_tot increased with increasing doping level.

To elucidate these phenomena, κ_latt and κ_elec were analyzed. κ_latt increased with the doping level and had a greater negative slope in the range of x = 0-0.05 than in the range of x = 0.075-0.125. In addition, κ_elec became more significant at higher doping levels. Therefore, according to the thermal conductivity relationship (κ_tot = κ_elec + κ_latt), the tendency of thermal conductivity was reversed at high temperatures.

The zT values of the Ni-doped FeSe₂ samples were calculated using the experimentally measured values of σ, S and κ_tot, and are shown in Fig 5. A zT of 0.11 was observed at x = 0.01 at 600 K, while the zT of other Ni-doped samples were 0.056-0.069 at 600 K. Even though the maximum zT shown for the pristine FeSe₂ sample (x = 0) at 600 K was not further enhanced by the Ni doping, despite the κ_latt decrease, the average zT (zT_avg) of the sample with x = 0.01 at all temperatures had the highest value of 0.029, as shown in the inset of Fig 5.

Fig. 5.

Thermoelectric figure of merit for the Fe_1-xNi_xSe₂ (x = 0, 0.01, 0.05, 0.075, 0.1, 0.125 and 0.2) samples as a function of temperature.

4. CONCLUSIONS

The thermoelectric properties of Ni-doped Fe_1-xNi_xSe₂ (x = 0, 0.01, 0.05, 0.075, 0.1, and 0.125) alloys were analyzed. Ni doping in FeSe₂ alloys induced n-type conduction over the entire temperature range, as FeSe₂ alloys exhibited both ntype and p-type conduction at different temperatures. Further, the electrical conductivity increased by approximately 40 times, from 8.52 (x = 0) to 329 S/cm (x = 0.125), with the increase in carrier concentration. In addition, the activation energy decreased with increasing doping levels, and the effective mass was maximized at x = 0.1. Therefore, the average power factor at x = 0.1 had the highest value except for undoped FeSe₂. The total thermal conductivity was decreased by Ni doping, from 6.81 to 4.29 W/mK, while the lattice thermal conductivity also decreased. Consequently, the sample with x = 0.1 had the highest average zT of approximately 0.029.

Article information Continued