
|
| ļ¬®ņĀü ļ░Å ļ▓öņ£ä Aims and Scope |
| ņĀĆļäÉ ņĀĢļ│┤ About the Journal |
| ĒÄĖņ¦æņ£äņøÉĒÜī Editorial Board |
| Open Access |
| ĒÄĖņ¦æĻĄŁ Editorial Office |


|
| ļ¬®ņĀü ļ░Å ļ▓öņ£ä Aims and Scope |
| ņĀĆļäÉ ņĀĢļ│┤ About the Journal |
| ĒÄĖņ¦æņ£äņøÉĒÜī Editorial Board |
| Open Access |
| ĒÄĖņ¦æĻĄŁ Editorial Office |

AbstractSnTe has drawn much attention due to its Pb-free composition along with tunable electronic and lattice structures. However, its intrinsically high defect concentration and high lattice thermal conductivity (╬║1) have hindered its application in devices. Recently, Bi doping at Sn-sites in Sn1-xBixTe (x = 0.0 ŌĆō 0.08) has been demonstrated to be effective in improving the thermoelectric performance (zT) of SnTe. Bi doping was particularly effective in improving the Seebeck coefficient in a wide range of temperature while suppressing its ╬║1. However, the effect of Bi doping on electronic band structure of SnTe has not been studied. Here, we applied the Single Parabolic Band (SPB) model to the room temperature electronic transport properties measurements (Seebeck coefficient, electrical conductivity, Hall carrier concentration) and analyzed how electronic band parameters like the density-of-states effective mass (md*), non-degenerate mobility (╬╝0), weighted mobility (╬╝w), and B-factor changes with a changing Bi doping content (x). As the x increases, the md* increases while ╬╝0 decreases. As the ╬╝w depends both on md* and ╬╝0, it peaks at x = 0.02. Lastly, the B-factor is related to the ratio of ╬╝w to ╬║1, due to significantly decreasing ╬║1 at high x, the B-factor also becomes the highest at x = 0.08. Based on the B-factor of x = 0.08 sample, the highest theoretical zT of 0.31 is predicted using the SPB model. This is approximately 2.2 times higher than the experimental zT (~0.139) reported in literature at 300 K. The SPB model also guides us that the highest theoretical zT of 0.31 can be achieved if its Hall carrier concentration is tuned to 9.06 ├Ś 1018 cm-3.
1. ņä£ ļĪĀUNņØ┤ ļ░£Ēæ£ĒĢ£ ņ¦ĆņåŹĻ░ĆļŖźļ░£ņĀäļ¬®Ēæ£ņŚÉ ļö░ļź┤ļ®┤ 13ļ▓łņ¦ĖļĪ£ ĻĖ░Ēøäļ│ĆĒÖöņÖĆ ĻĘĖļĪ£ ņØĖĒĢ£ ņśüĒ¢źņŚÉ ĻĖ┤ĻĖēĒĢśĻ▓ī ļīĆņØæĒĢśļŖö Ļ▓āņØä ļ¬®Ēæ£ļĪ£ ĒĢśĻ│Ā ņ׳ļŗż(ŌĆśClimate ActionŌĆÖ) [1]. ĻĖ░Ēøäļ│ĆĒÖö ļ¼ĖņĀ£ļŖö ņĀä ņäĖĻ│äņĀüņ£╝ļĪ£ ĒĢ©Ļ╗ś ĒÆĆņ¢┤ņĢ╝ ĒĢĀ ņĀä ņ¦ĆĻĄ¼ņĀüņØĖ ļ¼ĖņĀ£ņØ┤ļ®░ ņØ┤ļź╝ ĒĢ┤Ļ▓░ĒĢśĻĖ░ ņ£äĒĢ£ ļ░®ņĢł ņżæ ĒĢśļéśļŖö ņ╣£ĒÖśĻ▓Į ņŚÉļäłņ¦ĆņøÉņØś Ļ░£ļ░£ņØ┤ļŗż. ļŗżņ¢æĒĢ£ ņ╣£ĒÖśĻ▓Į ņŚÉļäłņ¦ĆņøÉļōżņØ┤ ņ׳ņ¦Ćļ¦ī ņŚ┤ņĀä ļ░£ņĀäņØĆ ņ¦ĆņåŹĻ░ĆļŖźĒĢ£ ņŚÉļäłņ¦Ć ĒĢśļ▓ĀņŖżĒīģ ĻĖ░ņłĀ ņżæ ĒĢśļéśļĪ£ ĒÅÉņŚ┤ņŚÉņä£ ņĀäĻĖ░ļź╝ ņāØņä▒ĒĢĀ ņłś ņ׳ļŖö ņ£Āļ¦ØĒĢ£ ĻĖ░ņłĀļĪ£ Ēśäņ×¼ ļ¦ÄņØĆ ņŚ░ĻĄ¼Ļ░Ć ņØ┤ļŻ©ņ¢┤ņ¦ĆĻ│Ā ņ׳ļŗż[2,3]. ņŚ┤ņĀä ļ░£ņĀä ĻĖ░ņłĀņØĆ ļ░śļÅäņ▓┤ ņåīņ×¼ ļé┤ ņś©ļÅä ņ░©ņØ┤ļĪ£ ņĀäņĢĢņØä ņ£ĀļÅä(ņĀäĒĢśņØś ņØ┤ļÅÖ)ĒĢśļŖö ņĀ£ļ▓Ī ĒÜ©Ļ│╝ļź╝ ņØ┤ņÜ®ĒĢ£ Ļ▓āņ£╝ļĪ£, ņØ┤ ĻĖ░ņłĀņØ┤ ļŹö ļäÉļ”¼ ĒÖ£ņÜ®ļÉśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņŚ┤ņĀä ļ░£ņĀä ņåīņ×ÉņØś ĒÜ©ņ£©ņØä ļåÆņŚ¼ ļŗżļźĖ ņŗĀņ×¼ņāØ ņŚÉļäłņ¦Ć ĒĢśļ▓ĀņŖżĒīģ ĻĖ░ņłĀ ļīĆļ╣ä Ļ▓Įņ¤üļĀźņØä ļåÆņŚ¼ņĢ╝ ĒĢ£ļŗż[4]. ņŚ┤ņĀä ļ░£ņĀä ĻĖ░ņłĀņØĆ ņ×¼ļŻīņ¦æņĢĮņĀüņØĖ ļČäņĢ╝ļĪ£ ņåīņ×ÉņØś ĒÜ©ņ£©ņØä ļåÆņØ┤ĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņåīņ×ÉņŚÉ ņĀüņÜ®ļÉśļŖö ņåīņ×¼ņØś ņŚ┤ņĀäņä▒ļŖźņØä ņ”ØļīĆņŗ£ņ╝£ņĢ╝ ĒĢ£ļŗż[5].
ņŚ┤ņĀäņåīņ×¼ņØś ņä▒ļŖźņØĆ ņŚ┤ņĀäņä▒ļŖźņ¦Ćņłś(zT)ņŚÉ ļö░ļØ╝ Ļ▓░ņĀĢļÉśļ®░, ņØ┤ļŖö ņåīņ×¼Ļ░Ć ņŚ┤ņØä ņĀäĻĖ░ļĪ£ ļ░öĻŠĖļŖö ņĀĢļ¤ēņĀüņØĖ ļŖźļĀźņØś ņ¦ĆĒæ£ļź╝ ņØśļ»ĖĒĢśļ®░ ļŗżņØīņØś ņŗØņ£╝ļĪ£ ņĀĢņØśļÉ£ļŗż[6-8].
ņŚ¼ĻĖ░ņä£ SļŖö ņĀ£ļ▓ĪĻ│äņłś, ŽāļŖö ņĀäĻĖ░ņĀäļÅäļÅä, TļŖö ņĀłļīĆņś©ļÅä, ╬║e ņÖĆ ╬║lņØĆ Ļ░üĻ░ü ņĀäĒĢśņŚÉ ņØśĒĢ£ ņŚ┤ņĀäļÅäļÅä ĻĖ░ņŚ¼ļČä ļ░Å Ļ▓®ņ×ÉņŚ┤ņĀäļÅäļÅäņØ┤ļŗż. zTļź╝ Ē¢źņāüņŗ£ĒéżĻĖ░ ņ£äĒĢ┤ņä£ļŖö S2Žā (=Power factor(PF))ļź╝ Ē¢źņāüņŗ£ĒéżĻ▒░ļéś, ╬║eņÖĆ ╬║lņØś ĒĢ®ņ£╝ļĪ£ ņĀĢņØśļÉśļŖö ņĀäņ▓┤ ņŚ┤ņĀäļÅäļÅä(╬║)ļź╝ Ļ░Éņåīņŗ£ņ╝£ņĢ╝ ĒĢ£ļŗż[9]. ĒĢśņ¦Ćļ¦ī, SņÖĆ Žā Ļ░äņØś ņĀäĒĢśļåŹļÅä ļ│ĆĒÖöņŚÉ ļö░ļźĖ ņāüņČ®Ļ┤ĆĻ│äļŖö PF Ē¢źņāüņØä ņ¢┤ļĀĄĻ▓ī ĒĢ£ļŗż. ļśÉĒĢ£, ╬║eļź╝ ļé«ņČöļĀżļŖö ļģĖļĀźņØĆ ŽāņÖĆ PFņØś Ļ░ÉņåīļĪ£ ņØ┤ņ¢┤ņ¦ł ņłś ņ׳ļŗż[10,11]. ļö░ļØ╝ņä£, zT Ē¢źņāüņØä ņ£äĒĢ£ ļīĆĒæ£ņĀüņØĖ ņŚ░ĻĄ¼ļ░®ļ▓Ģ ņ£╝ļĪ£ļŖö ļ░┤ļō£ĻĄ¼ņĪ░ ņĀ£ņ¢┤ļź╝ ĒåĄĒĢ┤ ŽāņØś Ļ░Éņåī ņŚåņØ┤ ņāüĒā£ļ░ĆļÅä ņ£ĀĒÜ©ņ¦łļ¤ē(md*)ņØś ņ”ØĻ░ĆļĪ£ Sļź╝ Ē¢źņāüņŗ£ĒéżļŖö ļ░®ļ▓Ģ(PFņØś ņ”ØĻ░Ć)Ļ│╝ Ļ▓░ņĀĢĻĄ¼ņĪ░ņØś ļ│Ąņ×Īņä▒ ņ”ØĻ░Ć ļ░Å ļéśļģĖĻĄ¼ņĪ░ĒÖö ņĀäļץ ļō▒ņØä ĒåĄĒĢ┤ ╬║lņØä ņäĀĒāØņĀüņ£╝ļĪ£ Ļ░Éņåīņŗ£ĒéżļŖö ļ░®ļ▓ĢņØ┤ ņ׳ļŗż[12]. ╬║lņØĆ zT ļé┤ ļŗżļźĖ ņØĖņ×É(parameter)ņŚÉ ņśüĒ¢źņØä ņŻ╝ņ¦Ć ņĢŖņ£╝ļ®┤ņä£ ļé«ņČ£ ņłś ņ׳ļŖö ņ£ĀņØ╝ĒĢ£ ņØĖņ×ÉņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ, Ēżļģ╝ ņé░ļ×ĆņŚÉ ņØśĒĢ£ ╬║l Ļ░ÉņåīļŖö Ļ░Ćņן ĒÖĢņŗżĒĢ£ zT ņ”ØļīĆ ņĀäļץ ņżæ ĒĢśļéśņØ┤ļŗż.
Ēśäņ×¼ ņŚ┤ņĀä ļ░£ņĀä ņåīņ×Éļź╝ ĒÖ£ņÜ®ĒĢ£ ĻĖ░ņłĀņØĆ ĻĖ░ņĪ┤ ņŚ┤ņĀäņåīņ×¼ ļé┤ ĒżĒĢ©ļÉ£ ļÅģņä▒ņØä ņ¦Ćļŗī ņøÉņåīĻ░Ć ļŗżļźĖ ļ¼┤ļÅģņä▒ ņøÉņåīļĪ£ ļīĆņ▓┤ļÉśĻ▒░ļéś, ņåīņ×ÉņØś ļé«ņØĆ ņŚ┤-ņĀäĻĖ░ ļ│ĆĒÖś ĒÜ©ņ£©ņØä ĻĘ╣ļ│ĄĒĢśĻĖ░ ņĀäĻ╣īņ¦ĆļŖö ņŚ¼ļ¤¼ ņØæņÜ® ļČäņĢ╝ņŚÉņä£ ļīĆĻĘ£ļ¬©ļĪ£ ņé¼ņÜ®ļÉśĻĖ░ ņ¢┤ļĀĄļŗż[13,14]. ĻĘĖļ¤¼ļ»ĆļĪ£ ņāłļĪ£ņÜ┤ ņ╣£ĒÖśĻ▓Į, Ļ│ĀĒÜ©ņ£© ņŚ┤ņĀäņåīņ×¼ņØś Ļ░£ļ░£ņØ┤ ņŗ£ĻĖēĒĢśļŗż. ņŚ░ĻĄ¼ ņżæņØĖ ņŚ¼ļ¤¼ ņŚ┤ņĀäņåīņ×¼ ņżæ SnTeļŖö ļÅģņä▒ņØ┤ ļé«ņØĆ ņåīņ×¼ļź╝ ņé¼ņÜ®ĒĢ£ļŗżļŖö ņĀÉĻ│╝, PbTeņÖĆ ļÅÖņØ╝ĒĢ£ rock salt ĻĄ¼ņĪ░ļź╝ ļéśĒāĆļé┤ĻĖ░ ļĢīļ¼ĖņŚÉ Ļ▓®ņ×É ļ░Å ņĀäņ×ÉĻĄ¼ņĪ░ ņĀ£ņ¢┤Ļ░Ć Ļ░ĆļŖźĒĢśļŗżĻ│Ā ņĢīļĀżņĀĖ ņ׳ņ¢┤ Ļ░Ćņן ņ£Āļ¦ØĒĢ£ lead-free ņŚ┤ņĀäņåīņ×¼ ļīĆņĢł ņżæ ĒĢśļéśļĪ£ ņŚ░ĻĄ¼ļÉśĻ│Ā ņ׳ļŗż[15,16]. ļÅäĒĢæņØ┤ ļÉśņ¦Ć ņĢŖņØĆ ņł£ņłś SnTeļŖö ļŗżņØ┤ļĀēĒŖĖ Ļ░Ł ļ░śļÅäņ▓┤(Eg = 0.18 eV)ļĪ£ ņóüņØĆ ļ░┤ļō£Ļ░Ł ļ░Å ļåÆņØĆ Ļ▓░ĒĢ© ļåŹļÅäļĪ£ PbTeņŚÉ ļ╣äĒĢ┤ ņŚ┤ņĀäņä▒ļŖźņØ┤ ļé«ļŗż[17,18]. SnTeņØś ļé«ņØĆ ņŚ┤ņĀäņä▒ļŖźņØĆ ņŻ╝ļĪ£ ļ¦ÄņØĆ ņłśņØś Sn Ļ│ĄĻ│Ą(ļåÆņØĆ ņĀäĒĢś ļåŹļÅä, nH=1020~1021cm3)ņ£╝ļĪ£ ņØĖĒĢ£ ļé«ņØĆ SņÖĆ, ļåÆņØĆ ņŚ┤ņĀäļÅäļÅä ļĢīļ¼ĖņØ┤ļØ╝Ļ│Ā ņĢīļĀżņĀĖ ņ׳ļŗż[19-21].
SnTeņØś ļé«ņØĆ ņŚ┤ņĀäņä▒ļŖźņØä ĻĘ╣ļ│ĄĒĢśĻĖ░ ņ£äĒĢ┤ Tan et al.ņØĆ InļÅäĒĢæņØä ĒåĄĒĢ┤ SnTeņØś Ļ░ĆņĀäņ×ÉļīĆ ļé┤ļČĆņŚÉ resonant stateļź╝ ņ£ĀļÅäĒĢ©ņ£╝ļĪ£ņŹ© ņĀĆņś©ņŚÉņä£ ņāüļŗ╣Ē׳ Ļ░£ņäĀļÉ£ Sļź╝ ļ│┤Ļ│ĀĒ¢łļŗż[22]. ĻĘĖ ņÖĖņŚÉļÅä, ļæÉ Ļ░ĆņĀäņ×ÉļīĆņØś ņłśļĀ┤(band convergence) ļ░Å ļÅäĒĢæ(Hg, Mn, ļ░Å Cd)ņØä ĒåĄĒĢ£ ļ░┤ļō£Ļ░Ł ņ”ØĻ░Ćļź╝ ĒåĄĒĢ┤ SnTeņØś Sļź╝ Ē¢źņāüĒĢĀ ņłś ņ׳ļŗż[12,16,23,24]. SnTeņØś PF ņ”ØļīĆ ļ┐É ņĢäļŗłļØ╝, SnTe ĒÖöĒĢ®ļ¼╝ņØś ╬║lņØä ļé«ņČöĻĖ░ ņ£äĒĢ£ ļģĖļĀźļÅä ņØ┤ļŻ©ņ¢┤ņĪīļŗż. ņśłļź╝ ļōżņ¢┤, CdS, HgTe ļ░Å ZnSņÖĆ Ļ░ÖņØĆ ļéśļģĖņ×ģņ×Éļź╝ SnTeņŚÉ ļÅäņ×ģĒĢśņŚ¼ ļéśļģĖņ×ģņ×ÉņŚÉ ņØśĒĢ£ Ēżļģ╝ ņé░ļ×Ćņ£╝ļĪ£ ╬║lņØä Ļ░Éņåīņŗ£ĒéżļŖö ņŚ░ĻĄ¼ļōżņØ┤ ņØ┤ļŻ©ņ¢┤ņĪīļŗż[18,25]. 2016ļģä Zhou et al.ņØĆ SnTe ņŚ┤ņĀäņåīņ×¼ņŚÉ Bi ņøÉņåīļź╝ ļÅäĒĢæĒĢ©ņ£╝ļĪ£ņŹ© ļäōņØĆ ņś©ļÅä ļ▓öņ£äņŚÉņä£ SĻ░Ć ņ”ØĻ░ĆĒĢśĻ│Ā, ļÅÖņŗ£ņŚÉ ╬║lņØ┤ Ēü¼Ļ▓ī Ļ░ÉņåīļÉśļŖö Ļ▓░Ļ│╝ļź╝ ļ│┤Ļ│ĀĒĢśņśĆļŗż. Bi ļÅäĒĢæļ¤ēņØ┤ 4 at.% ņØ┤ņāüņØ╝ ļĢī, SnTe ļé┤ Bi ņøÉņåīņØś ļÅäĒĢæĒĢ£Ļ│äņŚÉ ļÅäļŗ¼ĒĢśĻ▓ī ļÉśĻ│Ā, ļÅäĒĢæĒĢ£Ļ│ä ņØ┤ņāüņ£╝ļĪ£ ņČöĻ░ĆĒĢ£ Bi ņøÉņåīļŖö SnTe Ļ▓®ņ×É ļé┤ ņ╣©ņĀäļÉ£ļŗż. ļÅäĒĢæ ļ░Å ņ╣©ņĀäļÉ£ Bi ņøÉņåīļŖö SnTeņØś ņĀäĻĖ░ ļ░Å ņŚ┤ ņĀäļŗ¼ ĒŖ╣ņä▒ņØä ņĀ£ņ¢┤ĒĢśļŖö ļŹ░ ņżæņÜöĒĢ£ ņŚŁĒĢĀņØä Ē¢łļŗż. Bi ņøÉņåīņØś SnTe ļé┤ ļÅäĒĢæ/ņ╣©ņĀäņØś ĒÜ©Ļ│╝ļĪ£ 873 KņŚÉņä£ 1.1ņØś ņĄ£ļīĆ zT(ņĪ░ņä▒: Sn0.94Bi0.06Te)ļź╝ ļŗ¼ņä▒ĒĢĀ ņłś ņ׳ņŚłņ£╝ļ®░, ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆ ņł£ņłś SnTeņÖĆ ļ╣äĻĄÉĒĢśņŚ¼ zTĻ░Ć ņĢĮ 165 % Ē¢źņāüļÉśņŚłļŗż[26]. ĒĢśņ¦Ćļ¦ī Bi ļÅäĒĢæņ£╝ļĪ£ ņØĖĒĢ£ SnTeņØś ņĀäĻĖ░ņĀü ļ░┤ļō£ ņØĖņ×É ļ│ĆĒÖöņŚÉ ļīĆĒĢ£ ņŚ░ĻĄ¼ļŖö Ēśäņ×¼Ļ╣īņ¦Ć ļ│┤Ļ│ĀļÉ£ ļ░öĻ░Ć ņŚåļŗż.
ļö░ļØ╝ņä£, ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Bi ļÅäĒĢæņØ┤ SnTe ņŚ┤ņĀäņåīņ×¼ņØś ļ░┤ļō£ ņØĖņ×ÉņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä Ļ│Āņ░░ĒĢśņśĆļŗż. S, Žā, ╬║e, PF, ļ░Å zTņÖĆ Ļ░ÖņØ┤ ņåīņ×¼ņØś ņĀäĒĢśļåŹļÅäņŚÉ ļö░ļØ╝ ļ│ĆĒĢśļŖö ņØĖņ×ÉņÖĆ ļŗ¼ļ”¼, ļ░┤ļō£ ņØĖņ×ÉļŖö ņåīņ×¼ Ļ│Āņ£ĀņØś ĒŖ╣ņä▒ņØä ņ¦üņĀæņĀüņ£╝ļĪ£ ļ░śņśüĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ Bi ļÅäĒĢæ ĒÜ©Ļ│╝ļź╝ ļŹöņÜ▒ ļ¬ģĒÖĢĒĢśĻ▓ī ĒīÉļŗ©ĒĢĀ ņłś ņ׳ļŗż. Zhou et al.ņØś ĻĖ░ņĪ┤ ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ļź╝ ĻĖ░ļ░śņ£╝ļĪ£ 300KņŚÉņä£ Sn1-xBixTe (x=0, 0.02, 0.04, 0.06, 0.08)ņØś ļ░┤ļō£ ņØĖņ×ÉņØĖ ņāüĒā£ļ░ĆļÅä ņ£ĀĒÜ© ņ¦łļ¤ē(md*), ļ╣äņČĢĒć┤ņØ┤ļÅÖļÅä(╬╝0), Ļ░ĆņżæņØ┤ļÅÖļÅä(╬╝w) ļ░Å B-factorļź╝ Single Parabolic Band(SPB) ļ¬©ļŹĖņØä ĒåĄĒĢ┤ Ļ│äņé░Ē¢łļŗż[26]. Bi ļÅäĒĢæņØ┤ Ļ░üĻ░üņØś ļ░┤ļō£ ņØĖņ×ÉņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ļČäņäØĒĢśĻ│Ā, Ļ│äņé░ļÉ£ ļ░┤ļō£ ņØĖņ×ÉļōżņØä ĒåĄĒĢ┤ ņøÉņåīĻ░Ć ļÅäĒĢæļÉ£ SnTe ņåīņ×¼ ļé┤ņŚÉņä£ ņ¢╗ņØä ņłś ņ׳ļŖö Ļ░Ćņן ļåÆņØĆ ņØ┤ļĪĀ zT ļ░Å ņØ┤ zTļź╝ ĻĄ¼ĒśäĒĢĀ ņłś ņ׳ļŖö ņØ┤ļĪĀ ņĀäĒĢśļåŹļÅäļź╝ ņĀ£ņŗ£ĒĢśņśĆļŗż.
2. ņŗżĒŚś ļ░®ļ▓ĢSPB ļ¬©ļŹĖņØĆ ņåīņ×¼ņØś ļ░┤ļō£Ļ░Ć ļŗ©ņØ╝ Ēżļ¼╝ņäĀņØś ĒśĢĒā£ļĪ£ ļéśĒāĆļé£ļŗżļŖö Ļ░ĆņĀĢņØä ļ░öĒāĢņ£╝ļĪ£ ļ░┤ļō£ ņØĖņ×Éļź╝ ĒĢ┤ņäØĒĢśļŖö ļ¬©ļŹĖļĪ£ Ļ░üĻ░üņØś ļ░┤ļō£ ņØĖņ×ÉļŖö ļŗżņØīņØś Ļ│╝ņĀĢņØä ĒåĄĒĢ┤ Ļ│äņé░ļÉśņŚłļŗż. ņĀ£ļ▓ĪĻ│äņłś(S)ļŖö ņĢäļלņØś ņŗØņ£╝ļĪ£ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż[10,27,28]. ņŚ¼ĻĖ░ņä£ kB, e, ╬Ę, Fj(╬Ę)ļŖö Ļ░üĻ░ü ļ│╝ņĖĀļ¦ī ņāüņłś, ņĀäĒĢśļ¤ē, ĒÄśļź┤ļ»Ė ņżĆņ£ä, ņ░©ņłś jņŚÉ ļīĆĒĢ£ ĒÄśļź┤ļ»Ė ņĀüļČäņØ┤ļŗż(ņŗØ (3)) [10].
ņĀäĒĢś ļåŹļÅä(nH)ļŖö ╬ĘņÖĆ ņāüĒā£ļ░ĆļÅä ņ£ĀĒÜ©ņ¦łļ¤ē(md*)ņØä ņØ┤ņÜ®ĒĢ┤ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż[10]. ņŚ¼ĻĖ░ņä£ TņÖĆ hļŖö Ļ░üĻ░ü ņĀłļīĆņś©ļÅäņÖĆ Ēöīļ×æĒü¼ ņāüņłśņØ┤ļŗż.
ņŗØ (2,3)ņŚÉ ļö░ļź┤ļ®┤ SļŖö ╬ĘņŚÉļ¦ī ņØśņĪ┤ĒĢśļ»ĆļĪ£ ņĖĪņĀĢļÉ£ SĻ░ÆļōżņØä ņØ┤ņÜ®ĒĢśļ®┤ xņŚÉ ļö░ļźĖ Ļ░üĻ░üņØś ╬Ęļź╝ ņČöņĀĢĒĢĀ ņłś ņ׳ļŗż. ņČöņĀĢļÉ£ ╬Ęļź╝ ņŗØ (4)ņŚÉ ļīĆņ×ģĒĢśņŚ¼ nHņØś ņØ┤ļĪĀĻ░ÆĻ│╝ ņŗżĒŚśĻ░ÆņØ┤ Ļ░ÖņĢäņ¦ĆļÅäļĪØ md*Ļ░ÆņØä Ēö╝ĒīģĒĢśļ®┤ xņŚÉ ļö░ļźĖ Ļ░üĻ░üņØś md*ļź╝ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż.
╬╝HļŖö ļ╣äņČĢĒć┤ ņØ┤ļÅÖļÅä(╬╝0)ņÖĆ ╬Ęļź╝ ņØ┤ņÜ®ĒĢ┤ ņĢäļלņØś ņŗØņ£╝ļĪ£ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż[10]. ╬╝HļŖö ╬╝0ņÖĆ ╬ĘņŚÉ ņØśņĪ┤ĒĢśļ»ĆļĪ£ ņĢ×ņä£ Bi ļÅäĒĢæļ¤ē(x)ņŚÉ ļö░ļźĖ S ņĖĪņĀĢĻ░ÆņØä ĒåĄĒĢ┤ Ļ│äņé░ĒĢ£ ╬Ęļź╝ ņŗØ (5)ņŚÉ ļīĆņ×ģĒĢ£ Ēøä, ╬╝HņØś ņØ┤ļĪĀĻ░ÆĻ│╝ ņŗżĒŚśĻ░ÆņØ┤ Ļ░ÖņĢäņ¦ĆļÅäļĪØ ╬╝0Ļ░ÆņØä Ēö╝ĒīģĒĢśņŚ¼ xņŚÉ ļö░ļźĖ ╬╝0ļ│ĆĒÖöļź╝ Ļ│äņé░ĒĢśņśĆļŗż.
Ļ░ĆņżæņØ┤ļÅÖļÅä ╬╝wļŖö ņŚ┤ņĀäņ×¼ļŻīņØś ņĀäĻĖ░ņĀü ĒŖ╣ņä▒ņØä ļīĆļ│ĆĒĢśļŖö ļ░┤ļō£ ņØĖņ×ÉļĪ£ ╬╝0ņŚÉ md*ņØś Ļ░Ćņżæņ╣śļź╝ ņżĆ ĒśĢĒā£ņØĖ ņĢäļלņØś ņŗØņ£╝ļĪ£ ņĀĢņØśĒĢĀ ņłś ņ׳ļŗż[29].
B-factorļŖö ņĢäļלņØś ņŗØ (7)Ļ│╝ Ļ░ÖņØ┤ ņĀĢņØśļÉ£ļŗż[10].
3. Ļ▓░Ļ│╝ ļ░Å Ļ│Āņ░░
ĻĘĖļ”╝ 1(a)ņØś ļÅäĒśĢ(filled symbol)ņØĆ Zhou et al.ņØ┤ ļ│┤Ļ│ĀĒĢ£ Bi ļÅäĒĢæļ¤ē(x= 0 ’ĆŁ 0.08)ņŚÉ ļö░ļźĖ Sn1-xBixTeņØś nH ļ░Å SņØś ļ│ĆĒÖöļź╝ ļéśĒāĆļéĖļŗż[26]. xĻ░Ć ņ”ØĻ░ĆĒĢĀņłśļĪØ nHļŖö Ļ░ÉņåīĒĢśĻ│Ā SļŖö ņ”ØĻ░ĆĒĢśļŖö Ļ▓ĮĒ¢źņØä ļ│╝ ņłś ņ׳ļŗż. Bi ļÅäĒĢæļ¤ē(x)ņŚÉ ļö░ļźĖ md*ņØś ļ│ĆĒÖöļź╝ ļČäņäØĒĢśĻĖ░ ņ£äĒĢ┤ Single Parabolic Band(SPB) ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ĻĖ░ņĪ┤ ņŗżĒŚśĻ▓░Ļ│╝(filled symbol)ņŚÉ md*ļź╝ Ēö╝ĒīģĒĢśņśĆļŗż. md*ļŖö SPB ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŖö ņŚ┤ņĀäņåīņ×¼ņØś ņŻ╝ņÜö ļ░┤ļō£ ņØĖņ×Éļōż ņżæ ĒĢśļéśņØ┤ļ®░, ņĀäņ×É ļ░┤ļō£ ĻĄ¼ņĪ░ ļ░Å ņĀäņ×É ņāüĒā£ ļ░ĆļÅäņÖĆ Ļ░ÖņØĆ ņåīņ×¼ņØś ļ¼╝ļ”¼ņĀü ņåŹņä▒ņØä ņäżļ¬ģĒĢśļŖö ļŹ░ ņé¼ņÜ®ļÉ£ļŗż. md*ļź╝ Ēö╝ĒīģĒĢśņŚ¼ Ļ│äņé░ĒĢ£ nHļ│ĆĒÖöņŚÉ ļö░ļźĖ SļŖö ĻĘĖļ”╝ 1(a) ļé┤ ņŗżņäĀ(solid line)ņ£╝ļĪ£ Ēæ£ņŗ£ĒĢśņśĆļŗż. ĻĘĖļ”╝ 1(a) ņŚÉņä£ Ēö╝ĒīģĒĢ£ md*ļŖö ĻĘĖļ”╝ 1(b)ņŚÉ ļÅäĒśĢ(empty symbol)ļĪ£ Ēæ£ņŗ£ĒĢśņśĆļŗż. ĻĘĖļ”╝ 1(b)ņŚÉ ļö░ļź┤ļ®┤ Bi ļÅäĒĢæļ¤ēņØ┤ ņ”ØĻ░ĆĒĢĀņłśļĪØ(x= 0 - 0.08) md*Ļ░Ć ņ”ØĻ░ĆĒĢśļŖö Ļ▓ĮĒ¢źņØä Ļ┤Ćņ░░ĒĢĀ ņłś ņ׳ļŗż. Ļ░Ćņן ļåÆņØĆ md*(~0.66 m0)ņØä Ļ░Ćņ¦ĆļŖö Sn0.92Bi0.08TeņØś Ļ▓ĮņÜ░ ļ¬©ņāü SnTeņØś md*(~0.18 m0) ļīĆļ╣ä ņĢĮ 3.6ļ░░ ļåÆņØĆ Ļ▓░Ļ│╝ļź╝ ļ│┤ņśĆļŗż(m0 ļŖö ņĀäņ×ÉņØś ņĀĢņ¦Ć ņ¦łļ¤ē(electron rest mass)ņ×ä).
ĻĘĖļ”╝ 1(c)ņØś ļÅäĒśĢ(filled symbol)ņØĆ Zhou et al.ņØ┤ ņŗżĒŚś Ļ▓░Ļ│╝ļĪ£ ļ│┤Ļ│ĀĒĢ£ xņŚÉ ļö░ļźĖ Sn1-xBixTeņØś ╬╝Hļź╝ nHņŚÉ ļīĆĒĢśņŚ¼ Ēæ£ĒśäĒĢ£ Ļ▓āņØ┤ļŗż[26]. ņŗżĒŚśņĀüņ£╝ļĪ£ xĻ░Ć ņ”ØĻ░ĆĒĢĀņłśļĪØ ╬╝HĻ░Ć Ļ░ÉņåīĒĢśļŖö Ļ▓ĮĒ¢źņØ┤ ļéśĒāĆļé¼ļŗż. ņŗØ (4,5)ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ĻĖ░ņĪ┤ņŚÉ x ļ│ĆĒÖöņŚÉ ļö░ļØ╝ Ēö╝ĒīģĒĢ£ md*ļź╝ Ļ│ĀņĀĢĒĢ£ ņāüĒā£ņŚÉņä£, ╬╝HņŗżĒŚśĻ▓░Ļ│╝ņŚÉ ╬╝0ļź╝ Ēö╝ĒīģĒĢśņśĆļŗż. ╬╝0ļŖö ĒÄśļź┤ļ»Ė ņżĆņ£äĻ░Ć Ļ░ĆņĀäņ×ÉļīĆ ļśÉļŖö ņĀäļÅäļīĆņŚÉņä£ ņāüļŗ╣Ē׳ ļČäļ”¼ļÉ£ ņāüĒā£ ņ”ē, ņČĢĒć┤ļÉśņ¦Ć ņĢŖņØĆ ņāüĒā£ņŚÉņä£ņØś ņĀäĒĢśņØś ņØ┤ļÅÖļÅäļź╝ ļéśĒāĆļéĖļŗż. SPB ļ¬©ļŹĖ ĒĢ┤ņäØņŚÉņä£ ╬╝0ļŖö Ļ▓░ĒĢ©ņØ┤ļéś ļČłņł£ļ¼╝ļĪ£ ņØĖĒĢ£ ņé░ļ×Ć ĒśäņāüņØ┤ ņŚåņØä ļĢīņØś ņĀäĒĢśņØś ņØ┤ļÅÖņä▒ņØä ļéśĒāĆļéĖļŗż. ļö░ļØ╝ņä£ ╬╝0ļŖö ņ×¼ļŻīņØś Ļ│Āņ£ĀņØś ņØ┤ļÅÖļÅäļź╝ ļīĆļ│ĆĒĢśļŖö ļ░┤ļō£ ņØĖņ×ÉļĪ£ ņ×¼ļŻīņØś ĻĖ░ļ│ĖņĀüņØĖ ņĀäĒĢś ņØ┤ļÅÖ ĒŖ╣ņä▒ņØä ņØ┤ĒĢ┤ĒĢśļŖö ļŹ░ ņżæņÜöĒĢśļŗż. ĻĘĖļ”╝ 1(b)ņŚÉ ļéśĒāĆļéĖ xņŚÉ ļö░ļźĖ md*ņŚÉ ņāłļĪŁĻ▓ī Ēö╝ĒīģĒĢ£ ╬╝0ļĪ£ Ļ│äņé░ĒĢ£ nHņŚÉ ļö░ļźĖ ╬╝H Ļ│äņé░Ļ▓░Ļ│╝ļź╝ ĻĘĖļ”╝ 1(c)ņŚÉ ņŗżņäĀņ£╝ļĪ£ ļéśĒāĆļāłļŗż. ĻĘĖļ”╝ 1(c)ņØś ņŗżņäĀņØä Ļ│äņé░ĒĢśļŖöļŹ░ ņé¼ņÜ®ļÉ£ Ēö╝ĒīģļÉ£ ╬╝0 Ļ░ÆņØĆ ĻĘĖļ”╝ 1(d)ņŚÉ ļéśĒāĆļāłļŗż. ĻĘĖļ”╝ 1(d) ņŚÉ ļö░ļź┤ļ®┤, Bi ļÅäĒĢæļ¤ēņØ┤ ņ”ØĻ░ĆĒĢĀņłśļĪØ(x= 0 - 0.08) ╬╝0Ļ░Ć Ļ░ÉņåīĒĢśļŖö Ļ▓ĮĒ¢źņØä ļ│╝ ņłś ņ׳ļŗż. ņśłļź╝ ļōżņ¢┤, Biļź╝ ļÅäĒĢæĒĢśņ¦Ć ņĢŖņØĆ ņāśĒöī(x= 0.0)ņØĆ ╬╝0 Ļ░Æņ£╝ļĪ£ 1688 cm2s-1V-1ņØś Ēü░ Ļ░ÆņØä Ļ░Ćņ¦ĆļŖö ļ░śļ®┤ Bi ļÅäĒĢæļ¤ēņØ┤ Ļ░Ćņן ļ¦ÄņØĆ Sn0.92Bi0.08Te ņāśĒöī (x= 0.08)ņØś Ļ▓ĮņÜ░ ╬╝0Ļ░Ć 234.5 cm2s-1V-1Ļ╣īņ¦Ć Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż.
ļ¦īņĢĮ, x ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ md*ņØś ļ│ĆĒÖöĻ░Ć ņ×æņĢśļŗżļ®┤, x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ ╬╝0Ļ░ÉņåīļĪ£ļČĆĒä░(ĻĘĖļ”╝ 1(d)) xņØś ņ”ØĻ░ĆĻ░Ć Ēżļģ╝Ļ│╝ ņĀäĒĢś Ļ░äņØś ņāüĒśĖņ×æņÜ®ņØä Ļ░ĢĒÖöņŗ£Ēé©ļŗżĻ│Ā ņŻ╝ņןĒĢĀ ņłś ņ׳ņŚłņØä Ļ▓āņØ┤ļŗż. ĒĢśņ¦Ćļ¦ī ╬╝0ļŖö Ēżļģ╝Ļ│╝ ņĀäĒĢśņØś ņāüĒśĖņ×æņÜ®ņØä ņ¦üņĀæņĀüņ£╝ļĪ£ ļéśĒāĆļé┤ļŖö deformation ĒżĒģÉņģ£(Edef)Ļ│╝ md*ņŚÉ ļÅÖņŗ£ņŚÉ ņŚ░Ļ┤ĆļÉśņ¢┤ ņ׳ļŗż(╬╝0 ~ Edef-2 ├Ś md*-5/2). x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ md*ņØś ļ│ĆĒÖöļź╝ Ļ│ĀļĀżĒĢĀ Ļ▓ĮņÜ░, x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ ╬╝0ņØś Ļ░ÉņåīņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā x= 0.08 ņāśĒöīņØś EdefļŖö x= 0.0 ņāśĒöīņØś Edef ļīĆļ╣ä ņĢĮ 0.5ļ░░ ņ×æņĢśļŗż. Ļ▓░ĻĄŁ, Bi ļÅäĒĢæļ¤ēņØś ņ”ØĻ░ĆļŖö SnTe ļé┤ Ēżļģ╝Ļ│╝ ņĀäĒĢśĻ░äņØś ņāüĒśĖņ×æņÜ®ņØä ņĢĮĒÖöņŗ£Ēé© Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ļ│┤ĒåĄ Ēżļģ╝-ņĀäĒĢśĻ░ä ņāüĒśĖņ×æņÜ®ņØś Ļ░ÉņåīļŖö ņ”ØĻ░ĆļĪ£ ņØ┤ņ¢┤ņ¦äļŗż. ĒĢśņ¦Ćļ¦ī SnTeņŚÉ Biļź╝ ļÅäĒĢæĒĢśļŖö Ļ▓ĮņÜ░, md*Ļ░Ć ļÅÖņŗ£ņŚÉ ĻĖēĻ▓®ĒĢśĻ▓ī ņ”ØĻ░ĆĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ Ēżļģ╝-ņĀäĒĢśĻ░äņØś ņāüĒśĖņ×æņÜ®ņØś Ļ░ÉņåīņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā ╬╝0ļŖö Ļ░ÉņåīĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļČäņäØļÉśņŚłļŗż.
ĻĘĖļ”╝ 2ņŚÉļŖö Sn1-xBixTeņØś ņŚ┤ņĀäĒŖ╣ņä▒ ņżæ ņĀäĻĖ░ņĀäļÅäļÅä(Žā), ļĪ£ļĀīņĖĀ ņłś(L), ņĀäņ×ÉņŚ┤ņĀäļÅäļÅä(╬║e)ļź╝ ļéśĒāĆļé┤ņŚłļŗż. ŽāļŖö ņĢäļלņØś ņŗØņ£╝ļĪ£ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż[10]. ņŚ¼ĻĖ░ņä£ eļŖö ņĀäņ×ÉņØś ņĀäĒĢśļ¤ēņØ┤ļŗż.
ĻĘĖļ”╝ 2(a)ļŖö ĻĘĖļ”╝ 1ņŚÉņä£ Ļ│äņé░ĒĢ£ xņŚÉ ļö░ļźĖ md*ņÖĆ ╬╝0ņŚÉ ĻĖ░ļ░śĒĢśņŚ¼ SPB ļ¬©ļŹĖļĪ£ ņśłņĖĪĒĢ£ nHņŚÉ ļö░ļźĖ Žāļź╝ Ļ░üĻ░üņØś xņŚÉ ļīĆĒĢ┤ ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż (ņŗżņäĀ). ņØ┤ņŚÉ ļŹöĒĢśņŚ¼, nHņŚÉ ļö░ļźĖ Žā ņŗżĒŚśĻ░ÆņØä ļÅäĒśĢ(filled symbol)ņ£╝ļĪ£ Ēæ£ņŗ£ĒĢśņśĆļŗż[26]. ĻĘĖļ”╝ 1(c)ņŚÉņä£ xņØś ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ ╬╝HņÖĆ nHĻ░Ć ļÅÖņŗ£ņŚÉ Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŖöļŹ░, ╬╝HņÖĆ nHņØś Ļ│▒ņŚÉ ļ╣äļĪĆĒĢśļŖö Žā ņŚŁņŗ£, x ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä Ļ┤Ćņ░░ĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ”╝ 2(b)ļŖö ĻĘĖļ”╝ 2(a)ņŚÉ ņŗżņäĀņ£╝ļĪ£ ļéśĒāĆļéĖ SPB Ļ│äņé░ Ļ▓░Ļ│╝ ņżæ Ļ░ü ņāśĒöī(x)ņØś nHņĖĪņĀĢĻ░ÆņŚÉ ņāüņØæĒĢśļŖö ņØ┤ļĪĀ Žāļź╝ xņŚÉ ļīĆĒĢ┤ ņĀĢļ”¼ĒĢ£ Ļ▓░Ļ│╝ņØ┤ļŗż. Ļ│äņé░ Ļ▓░Ļ│╝ņÖĆ ņŗżĒŚśĻ░ÆņØä ĻĄ¼ļČäĒĢśĻĖ░ ņ£äĒĢ┤ ĻĘĖļ”╝ 2(a) ļé┤ Žā ņŗżĒŚśĻ░ÆņØĆ filled ļÅäĒśĢņØä ņé¼ņÜ®Ē¢łņ¦Ćļ¦ī, ĻĘĖļ”╝ 2(b) ļé┤ Žā Ļ│äņé░Ļ░ÆņØĆ open ļÅäĒśĢņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ĻĘĖļ”╝ 2(a)ņØś Žā ņŗżĒŚśĻ░ÆĻ│╝ ĻĘĖļ”╝ 2(b)ņØś Žā Ļ│äņé░Ļ░ÆņØ┤ Ļ▒░ņØś ļÅÖņØ╝ĒĢ£ Ļ▓āņØä ĒåĄĒĢ┤, ĻĘĖļ”╝ 1ņŚÉņä£ ņŗżĒŚśĻ▓░Ļ│╝ņŚÉ Ēö╝ĒīģĒĢ£ md*ņÖĆ ╬╝0ļ░┤ļō£ ņØĖņ×ÉĻ░Ć ņåīņ×¼ņØś ĒŖ╣ņä▒ņØä ņל ļ░śņśüĒĢ£ļŗżļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ”╝ 2(b)ņŚÉ ļö░ļź┤ļ®┤, x=0.08 ņāśĒöīņØś ŽāĻ░Ć ņł£ņłś SnTe(x=0.0) ņāśĒöī ļīĆļ╣ä ņĢĮ 88 % Ļ░ÉņåīĒĢ£ Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż (8700ŌåÆ 1000 Scm-1). Bi ļÅäĒĢæļ¤ē ņ”ØĻ░ĆņŚÉ ļö░ļźĖ Žā Ļ░ÉņåīļŖö Bi ļÅäĒĢæļ¤ēņØ┤ ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ ╬╝HņÖĆ nHņØ┤ ļÅÖņŗ£ņŚÉ Ļ░ÉņåīĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ ╬╝HĻ░ÉņåīļŖö Edef Ļ░Éņåīļź╝ ņāüņćäņŗ£Ēé¼ ļ¦īĒü╝ņØś md* ņ”ØĻ░ĆņŚÉ ĻĖ░ņØĖĒĢ£ļŗżĻ│Ā ņĢ×ņä£ ņäżļ¬ģĒĢ£ ļ░ö ņ׳ļŗż. ņØ┤ņŚÉ ļŹöĒĢśņŚ¼, x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ md* ņ”ØĻ░Ć(ĻĘĖļ”╝ 1(b))ņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā nHĻ░Ć Ļ░ÉņåīĒĢśļŖö ņØ┤ņ£ĀļŖö x ņ”ØĻ░ĆļĪ£ ņØĖĒĢ£ ĒÄśļź┤ļ»Ė ņżĆņ£ä(╬Ę)ņØś Ļ░Éņåī ļĢīļ¼Ėņ£╝ļĪ£ ĒĢ┤ņäØļÉĀ ņłś ņ׳ļŗż.
ĻĘĖļ”╝ 2(c)ņÖĆ 2(d)ļŖö Bi ļÅäĒĢæļ¤ēņŚÉ ļö░ļźĖ ļĪ£ļĀīņĖĀ ļäśļ▓ä(L)ņØś ļ│ĆĒÖöļź╝ ļČäņäØĒĢ£ Ļ▓āņØ┤ļŗż. SPB ļ¬©ļŹĖņŚÉ ļö░ļź┤ļ®┤ LņØĆ ņĢäļלņØś ņŗØņ£╝ļĪ£ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż[10].
ņŗØ (11)ņŚÉ ļö░ļź┤ļ®┤ LņØĆ ╬ĘņŚÉļ¦ī ņØśņĪ┤ĒĢśļŖö ĒĢ©ņłśņØĖ Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. LĻ│╝ ņ£Āņé¼ĒĢśĻ▓ī ╬ĘņŚÉļ¦ī ņØśņĪ┤ĒĢśļŖö SļĪ£ļČĆĒä░ ╬Ęļź╝ ņŚŁņ£╝ļĪ£ Ļ│äņé░ĒĢ┤ļé╝ ņłś ņ׳ļŗż (ņŗØ (2)). ļö░ļØ╝ņä£ ĻĘĖļ”╝ 1(a)ņŚÉ ņŗżņäĀņ£╝ļĪ£ Ēæ£ņŗ£ļÉ£ nHņŚÉ ļīĆĒĢ£ S Ļ│äņé░Ļ░Æņ£╝ļĪ£ļČĆĒä░ nHņŚÉ ļö░ļźĖ ╬Ęļź╝ Ļ│äņé░ĒĢśĻ│Ā, ĻĘĖ Ļ▓░Ļ│╝ļź╝ ņŗØ (10)ņŚÉ ļīĆņ×ģĒĢśņŚ¼ Bi ļÅäĒĢæļ¤ēņŚÉ ļö░ļźĖ L Ļ│äņé░Ļ░ÆņØä nHņŚÉ ļīĆĒĢśņŚ¼ ļéśĒāĆļé┤ņŚłļŗż (ĻĘĖļ”╝ 2(c)). ļÅÖņØ╝ĒĢ£ nHņŚÉņä£ xĻ░Ć ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ LņØ┤ Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä Ļ┤Ćņ░░ĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ”╝ 2(d)ļŖö ĻĘĖļ”╝ 2(c)ņŚÉņä£ Ļ│äņé░ĒĢ£ nHņŚÉ ļö░ļźĖ L ņżæ Ļ░ü ņāśĒöī(x)ņØś nHņĖĪņĀĢĻ░ÆņŚÉ ņāüņØæĒĢśļŖö ņØ┤ļĪĀ LņØä xņŚÉ ļīĆĒĢ┤ ņĀĢļ”¼ĒĢ£ Ļ▓░Ļ│╝ņØ┤ļŗż. xĻ░Ć ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ LņØ┤ ņäĀĒśĢņĀüņ£╝ļĪ£ Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņØ┤ļŖö ļśÉĒĢ£ x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ ╬ĘņØś Ļ░Éņåīļź╝ Ļ░äņĀæņĀüņ£╝ļĪ£ ļ│┤ņŚ¼ņżĆļŗż (md* ņ”ØĻ░ĆņŚÉļÅä nHĻ░Ć Ļ░ÉņåīĒĢśļŖö ņØ┤ņ£Ā).
ļ¦łņ¦Ćļ¦ēņ£╝ļĪ£, ĻĘĖļ”╝ 2(e)ņÖĆ 2(f)ļŖö ╬║eņŚÉ ļīĆĒĢ£ ļČäņäØ Ļ▓░Ļ│╝ļź╝ ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż. ╬║eļŖö ņĢäļלņØś ņŗØņ£╝ļĪ£ ļéśĒāĆļé╝ ņłś ņ׳ļŗż[10].
ņĢ×ņä£ SPB ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢ£ ŽāņÖĆ LņØä ņŗØ (12)ņŚÉ ļīĆņ×ģĒĢśņŚ¼ Ļ░üĻ░üņØś Bi ļÅäĒĢæ ĒĢ©ļ¤ēņŚÉ ļīĆĒĢ┤ nHņŚÉ ļö░ļźĖ ņØ┤ļĪĀ ╬║eļź╝ ĻĘĖļ”╝ 2(e)ņŚÉ ņŗżņäĀņ£╝ļĪ£ ļéśĒāĆļé┤ņŚłļŗż (Zhou et al.ņŚÉņä£ ļ│┤Ļ│ĀĒĢ£ ╬║e ņŗżĒŚśĻ░ÆņØä filled ļÅäĒśĢņ£╝ļĪ£ ĒĢ©Ļ╗ś Ēæ£ņŗ£ĒĢśņśĆļŗż) [26]. ņØ┤ļĪĀ ╬║e(ņŗżņäĀ)ņŚÉ ļö░ļź┤ļ®┤ xņÖĆ ņāüĻ┤ĆņŚåņØ┤ ļ¬©ļōĀ ņāśĒöīļōżņŚÉņä£ nHĻ░Ć ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ ņØ┤ļĪĀ ╬║e ņŚŁņŗ£ ņ”ØĻ░ĆĒĢśļŖö Ļ▓āņØä Ļ┤Ćņ░░ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļŖö nHņ”ØĻ░ĆņŚÉ ļīĆĒĢśņŚ¼ ņØ┤ļĪĀ Žā(ĻĘĖļ”╝ 2(a))ņÖĆ L(ĻĘĖļ”╝ 2(c)) ļ¬©ļæÉ ņ”ØĻ░ĆĒĢśļŖö Ļ▓āņŚÉ ĻĖ░ņØĖĒĢ£ļŗż (ņŗØ (11)). ĻĘĖļ”╝ 2(e) ļé┤ ņØ┤ļĪĀ ╬║e (ņŗżņäĀ) ņżæ Ļ░ü ņāśĒöīņØś ņŗżĒŚś nHņŚÉ ņāüņØæĒĢśļŖö ņØ┤ļĪĀ ╬║eļź╝ xņŚÉ ļīĆĒĢśņŚ¼ ļö░ļĪ£ ĻĘĖļ”╝ 2(f)ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. ĻĘĖļ”╝ 2(f)ņŚÉ ļö░ļź┤ļ®┤, Bi ļÅäĒĢæļ¤ēņØ┤ ņ”ØĻ░ĆĒĢĀņłśļĪØ ╬║eĻ░Ć Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. x ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ ņØ┤ļĪĀ Žā(ĻĘĖļ”╝ 2(b))ņÖĆ L(ĻĘĖļ”╝ 2(d))ņØ┤ ļ¬©ļæÉ Ļ░ÉņåīĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ x ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ ņØ┤ļĪĀ ╬║e ļśÉĒĢ£ Ļ░ÉņåīĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļČäņäØļÉ£ļŗż.
ĻĘĖļ”╝ 3(a)ļŖö ņŗØ (6)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢ£ Sn1-xBixTeņØś Ļ░ĆņżæņØ┤ļÅÖļÅä(Weighted mobility,)ļź╝ xņŚÉ ļīĆĒĢ┤ ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż. ╬╝wļŖö ĻĘĖļ”╝ 1(b)ņØś md*ņÖĆ ĻĘĖļ”╝ 1(d)ņØś ╬╝0ļź╝ ņØ┤ņÜ®ĒĢ┤ Ļ│äņé░ĒĢśņśĆļŗż. x= 0.02(~185 cm2s-1V-1), x= 0.04(~169 cm2s-1V-1) ņØ╝ ļĢī, ļŗżļźĖ ņāśĒöīļōżņŚÉ ļ╣äĒĢ┤ ņāüļīĆņĀüņ£╝ļĪ£ ļåÆņØĆ ╬╝wĻ░Ć ļéśĒāĆļé¼ļŗż. x ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ md*Ļ░Ć ņ”ØĻ░ĆĒĢśļŖö ļ░śļ®┤, ╬╝0ļŖö Ļ░ÉņåīĒĢśļŖö Ļ▓ĮĒ¢źņØä ĻĘĖļ”╝ 1ņŚÉņä£ ĒÖĢņØĖĒĢ£ ļ░ö ņ׳ļŗż. md*ņØś ņ”ØĻ░ĆļČä ļīĆļ╣ä, ╬╝0ņØś Ļ░ÉņåīļČäņØ┤ ļŹöņÜ▒ Ēü¼ĻĖ░ ļĢīļ¼ĖņŚÉ ╬╝wļŖö x= 0.02 ņāśĒöīņŚÉņä£ ņĄ£Ļ│ĀĻ░ÆņØä ļŗ¼ņä▒ĒĢ£ Ēøä x > 0.02 ņāśĒöīļōżņŚÉņä£ļŖö Ļ│äņåŹ Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä Ļ┤Ćņ░░ĒĢĀ ņłś ņ׳ļŗż. ņ£äņŚÉņä£ ņäżļ¬ģĒĢ£ Ļ▓āņ▓śļ¤╝ ╬╝wļŖö ņåīņ×¼ņØś ņØ┤ļĪĀ ņĄ£ļīĆ PFņÖĆ ņ¦üņĀæņĀüņ£╝ļĪ£ ņŚ░Ļ┤ĆļÉśņ¢┤ ņ׳ļŗż. ļŗżņŗ£ ļ¦ÉĒĢ┤, ╬╝wĻ░Ć Ļ░Ćņן Ēü░ x= 0.02 ņāśĒöīņŚÉņä£ nHĻ░Ć ņĄ£ņĀüņ£╝ļĪ£ ļ¦×ņČ░ņ¦ł Ļ▓ĮņÜ░, ļŗżļźĖ Sn1-xBixTe ņāśĒöī ļīĆļ╣ä Ļ░Ćņן ļåÆņØĆ PFļź╝ ļéśĒāĆļé╝ Ļ▓āņ£╝ļĪ£ ņśłņāüĒĢĀ ņłś ņ׳ļŗż.
ĻĘĖļ”╝ 3(b)ņØś ņŗżņäĀņØĆ ĻĘĖļ”╝ 3(a)ņŚÉņä£ Ļ│äņé░ĒĢ£ ╬╝Wļź╝ ĻĖ░ļ░śņ£╝ļĪ£ SPB ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢ┤ nHļ│ĆĒÖöņŚÉ ļö░ļźĖ ņØ┤ļĪĀ PF (= S2Žā)ļź╝ Ļ░üĻ░üņØś xņŚÉ ļīĆĒĢ┤ ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż. Ļ│äņé░ļÉ£ ╬╝wĻ░Ć Ļ░Ćņן ļé«ņØĆ x= 0.06 ņāśĒöīņØś Ļ▓ĮņÜ░ (╬╝W= 120 cm2s-1V-1), ņØ┤ļĪĀ ņĄ£ļīĆ PF ļśÉĒĢ£ ~36 ╬╝Wcm-1K-2ļĪ£ ļé«ļŗż. ĒĢśņ¦Ćļ¦ī Ļ│äņé░ļÉ£ ╬╝WĻ░Ć Ļ░Ćņן ļåÆņØĆ x= 0.02 ņāśĒöīņØś Ļ▓ĮņÜ░ (╬╝W= 185 cm2s-1V-1), ņØ┤ļĪĀ ņĄ£ļīĆ PF ļśÉĒĢ£ ~55 ╬╝Wcm-1K-2ļĪ£ Ļ░Ćņן ļåÆņĢśļŗż. ĒĢśņ¦Ćļ¦ī Zhou et al. ļ│┤Ļ│ĀĒĢ£ Sn1-xBixTeņØś PF ņŗżĒŚśĻ░ÆņŚÉ ļö░ļź┤ļ®┤ (ĻĘĖļ”╝ 3(b) ļé┤ filled ļÅäĒśĢ), PF ņŗżĒŚśĻ░ÆņØ┤ ņØ┤ļĪĀ PFņÖĆ Ēü░ ņ░©ņØ┤Ļ░Ć ņ׳ļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ņśłļź╝ ļōżņ¢┤, Zhou et al. ņØĆ x= 0.02 ņāśĒöīņØś 300 K PFļĪ£ 17 ╬╝Wcm-1K-2ļź╝ ļ│┤Ļ│ĀĒĢśņśĆļŗż. ĒĢśņ¦Ćļ¦ī ņČöĻ░ĆņĀüņØĖ ļÅäĒĢæņØä ĒåĄĒĢ┤ x= 0.02 ņāśĒöīņØś ņŗżĒŚś nHļź╝ 6├Ś 1018 cm-3ļĪ£ ĒŖ£ļŗØĒĢ£ļŗżļ®┤ ņĢĮ 3.2 ļ░░ņØś PF ņ”ØļīĆļź╝ ĻĖ░ļīĆĒĢĀ ņłś ņ׳ļŗż (17 ŌåÆ 55 ╬╝Wcm-1K-2).
ĻĘĖļ”╝ 3(c)ņŚÉļŖö ņŚ┤ņĀäņ×¼ļŻīņØś zTņÖĆ ņ¦üņĀæņĀüņ£╝ļĪ£ ņŚ░Ļ┤ĆņØ┤ ņ׳ļŖö ļ░┤ļō£ ņØĖņ×ÉņØĖ B-factorļź╝ Bi ļÅäĒĢæļ¤ē(x)ņŚÉ ļīĆĒĢ┤ ļéśĒāĆļé┤ņŚłļŗż (ņŗØ (7)). ņŗØ (7)ņŚÉ ļö░ļź┤ļ®┤ B-factorļŖö ╬╝WņÖĆ ╬║lĻ░äņØś ļ╣äņ£©ņŚÉ ļ╣äļĪĆĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ĻĘĖļ”╝ 3(c)ņØś B-factorļŖö x ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ ņäĀĒśĢņĀüņ£╝ļĪ£ ņ”ØĻ░ĆĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ļŗ©, x= 0.02 ņāśĒöīņØś Ļ▓ĮņÜ░, B-factorĻ░Ć x= 0.0, x= 0.04 ņāśĒöīļōżņØś Bfactor ļīĆļ╣ä ļåÆņØĆ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. B-factorņØś ņØ┤ļ¤¼ĒĢ£ Ļ▓ĮĒ¢źņØĆ ╬╝WņÖĆ ╬║lņØś x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ Ļ▓ĮĒ¢źņ£╝ļĪ£ ņäżļ¬ģļÉĀ ņłś ņ׳ļŗż. x= 0.02 ņāśĒöīņØś B-factorĻ░Ć x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ ņäĀĒśĢņĀüņØĖ B-factor ņ”ØĻ░Ć Ļ▓ĮĒ¢źņŚÉņä£ ļ▓Śņ¢┤ļéśņä£ x= 0.04 ņāśĒöīņØś B-factor ļ│┤ļŗż ļåÆņØĆ ņØ┤ņ£ĀļŖö x= 0.02 ņāśĒöīņØś ╬╝WĻ░Ć ļŗżļźĖ x ļīĆļ╣ä Ļ░Ćņן ļåÆņĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ĻĘĖ ņÖĖ x > 0.04 ņśüņŚŁņŚÉņä£ x ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ B-factorĻ░Ć ņ”ØĻ░ĆĒĢ£ ņØ┤ņ£ĀļŖö ĻĘĖļ”╝ 3(d)ņŚÉ ļéśĒāĆļéĖ ╬║lĻ░Ć x > 0.04 ņśüņŚŁņŚÉņä£ x ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ ĻĖēĻ▓®ĒĢśĻ▓ī Ļ░ÉņåīĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ĻĘĖļ”╝ 3(d)ņØś ╬║lļŖö Zhou et al.ņØ┤ ļ│┤Ļ│ĀĒĢ£ ņĀäņ▓┤ ņŚ┤ņĀäļÅäļÅä(╬║) ņĖĪņĀĢĻ░ÆņŚÉņä£ SPB ļ¬©ļŹĖļĪ£ Ļ│äņé░ĒĢ£ ╬║e (ĻĘĖļ”╝ 2(f))ļź╝ ņĀ£ĒĢśņŚ¼ Ļ│äņé░ĒĢśņśĆļŗż[26]. Bi ļÅäĒĢæļ¤ēņØ┤ x= 0.0ņŚÉņä£ 0.04Ļ╣īņ¦Ć ņ”ØĻ░ĆĒĢĀ ļĢī ╬║lņØś ļ│ĆĒÖöļ¤ēņØĆ ļ»Ėļ»ĖĒĢ£ Ļ▓āņØä Ļ┤Ćņ░░ĒĢĀ ņłś ņ׳ļŗż. ĒĢśņ¦Ćļ¦ī x > 0.04 ņśüņŚŁņŚÉņä£ x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ ╬║lĻ░ÉņåīĻ░Ć ĻĖēĻ▓®ĒĢśĻ▓ī ņØ╝ņ¢┤ļéśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. x= 0.04 ņØ╝ ļĢī, ~1.8 Wm-1K-1 ņØ┤ļŹś ╬║lĻ░Ć x= 0.08 ņØ╝ ļĢī ņĢĮ 1.13 Wm-1K-1 Ļ╣īņ¦Ć ņĢĮ 37 % Ļ░ÉņåīĒĢ£ļŗż.
ĻĘĖļ”╝ 4ļŖö ĻĘĖļ”╝ 3(c)ņŚÉņä£ Ļ│äņé░ĒĢ£ B-factorļź╝ ĻĖ░ļ░śņ£╝ļĪ£ SPB ļ¬©ļŹĖļĪ£ Ļ│äņé░ĒĢ£ nHņŚÉ ļö░ļźĖ ņØ┤ļĪĀ zT ļ│ĆĒÖö(ņŗżņĀä)ņÖĆ Zhou et al.ņØ┤ ļ│┤Ļ│ĀĒĢ£ zT ņĖĪņĀĢĻ░Æ(filled ļ¬©ņ¢æ)ņØä ļ│┤ņŚ¼ņżĆļŗż. ĻĘĖļ”╝ 3(c)ņŚÉ ļéśĒāĆļéĖ xņŚÉ ļö░ļźĖ B-factor Ļ░ÆĻ│╝ ĻĘĖļ”╝ 4ņŚÉ ļéśĒāĆļéĖ ņØ┤ļĪĀ zT ņĄ£ļīĆĻ░ÆĻ│╝ ļ╣äļĪĆĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ļŗżņŗ£ ļ¦ÉĒĢ┤, B-factorĻ░Ć Ļ░Ćņן ļé«ņØĆ x= 0.0 ņāśĒöī(Bfactor = 0.05)ņØś Ļ▓ĮņÜ░, ņØ┤ļĪĀ zT ņĄ£ļīĆĻ░Æ ļśÉĒĢ£ ņĢĮ 0.15ļĪ£ x ņżæ Ļ░Ćņן ļé«ņĢśļŗż. ĒĢśņ¦Ćļ¦ī, ĻĘĖļ”╝ 3(c)ņŚÉņä£ B-factorĻ░Ć Ļ░Ćņן ļåÆņĢśļŹś x= 0.08 ņāśĒöī(B-factor = 0.075)ņØś Ļ▓ĮņÜ░, ņØ┤ļĪĀ zT ņĄ£ļīĆĻ░Æ ļśÉĒĢ£ ņĢĮ 0.31ļĪ£ ņŚ¼ļ¤¼ x ņżæ Ļ░Ćņן ļåÆļŗż. ĻĘĖļ”╝ 4ņŚÉ ļö░ļź┤ļ®┤, SnTeņŚÉ Biļź╝ ļÅäĒĢæĒĢśļ®┤ ņł£ņłś SnTe ļīĆļ╣ä Ē¢źņāüļÉ£ zTļź╝ ņ¢╗ņØä ņłś ņ׳ļŗż (300K). x= 0.02, 0.04ņØĖ Ļ▓ĮņÜ░ ļåÆņØĆ ╬╝wņØś ņśüĒ¢źņ£╝ļĪ£ Ē¢źņāüļÉ£ zTĻ░Ć ļéśĒāĆļé¼ņ£╝ļ®░, x= 0.06, 0.08ņØś Ļ▓ĮņÜ░ Ēü¼Ļ▓ī Ļ░ÉņåīļÉ£ ╬║lņØś ņśüĒ¢źņ£╝ļĪ£ Ē¢źņāüļÉ£ zTĻ░Ć ļéśĒāĆļé¼ļŗż (ĻĘĖļ”╝ 3). ņØ┤ļĪĀņĀüņ£╝ļĪ£ 300 KņŚÉņä£ ņ¢╗ņØä ņłś ņ׳ļŖö zTņØś ņĄ£ļīōĻ░ÆņØĆ 0.311(x= 0.08)ļĪ£ Ļ│äņé░ļÉśņŚłņ£╝ļ®░, x= 0.02, 0.04, 0.06 ņŚŁņŗ£ Ļ░üĻ░ü 0.275, 0.268, 0.280ņ£╝ļĪ£ x= 0.0 (zT = 0.160)ņŚÉ ļ╣äĒĢ┤ ļåÆņØĆ ņØ┤ļĪĀ ņĄ£ļīĆ zTĻ░ÆņØä ļ│┤ņśĆļŗż. Zhou et al.ņØś ņŗżĒŚś zTĻ░Æ(filled ļ¬©ņ¢æ)Ļ│╝ SPB ļ¬©ļŹĖ Ļ▓░Ļ│╝ļź╝ ļ╣äĻĄÉĒĢ┤ļ│┤ļ®┤ x= 0.08 ņāśĒöīņØś nHļź╝ 9.06 ├Ś 1018 cm-3Ļ╣īņ¦Ć Ļ░Éņåīņŗ£ņ╝░ņØä ļĢī, ĻĖ░ņĪ┤ ņŗżĒŚś zT(= 0.139) ļīĆļ╣ä ņĢĮ 2.2ļ░░ Ē¢źņāüļÉ£ zT = 0.311ļź╝ ļŗ¼ņä▒ĒĢĀ Ļ▓āņ£╝ļĪ£ ņśłņĖĪļÉśņŚłļŗż.
4. Ļ▓░ ļĪĀļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Single Parabolic Band(SPB) ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢ┤ SnTeņŚÉ ļīĆĒĢ£ Bi ļÅäĒĢæ(x= 0.0 ŌĆō 0.08)ņØ┤ ņāüĒā£ļ░ĆļÅä ņ£ĀĒÜ©ņ¦łļ¤ē(md*), ļ╣äņČĢĒć┤ņØ┤ļÅÖļÅä(╬╝0), Ļ░ĆņżæņØ┤ļÅÖļÅä(╬╝w), B-factorņÖĆ Ļ░ÖņØĆ ļ░┤ļō£ ņØĖņ×ÉļōżņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä Ļ│Āņ░░ĒĢśņśĆļŗż. SnTeņŚÉ ļīĆĒĢ£ Bi ļÅäĒĢæņØĆ md*ļź╝ ņ”ØĻ░Ćņŗ£ĒéżĻ│Ā ╬╝0ļź╝ Ļ░Éņåīņŗ£ņ╝░ļŗż. ĻĘĖ Ļ▓░Ļ│╝, x= 0.02ņŚÉņä£ Ļ░Ćņן ļåÆņØĆ ╬╝W(185 cm2s-1V-1)ļź╝ ļéśĒāĆļé┤ļŖö Ļ▓āņ£╝ļĪ£ Ļ│äņé░ļÉśņŚłļŗż. ĒĢśņ¦Ćļ¦ī, x ņ”ØĻ░ĆņŚÉ ļö░ļźĖ Ļ▓®ņ×ÉņŚ┤ņĀäļÅäļÅä (╬║l) Ļ░ÉņåīļĪ£ B-factorņØś Ļ▓ĮņÜ░, x= 0.02Ļ░Ć ņĢäļŗī x= 0.08ņŚÉņä£ Ļ░Ćņן ļåÆĻ▓ī Ļ│äņé░ļÉśņŚłļŗż. B-factorļź╝ ĻĖ░ļ░śņ£╝ļĪ£ ĒÖĆ ņĀäĒĢśļåŹļÅä (nH)ņŚÉ ļö░ļźĖ ņØ┤ļĪĀ zT ļśÉĒĢ£ Ļ│äņé░ĒĢśņśĆļŗż. B-factorĻ░Ć Ļ░Ćņן ļåÆņĢśļŹś x= 0.08 ņāśĒöīņØś ņØ┤ļĪĀ zT ņĄ£ļīĆĻ░ÆņØĆ 0.311ļĪ£ ļŗżļźĖ ņāśĒöīļōż ļīĆļ╣ä Ļ░Ćņן ļåÆĻ▓ī Ļ│äņé░ļÉśņŚłļŗż. ņØ┤ ņØ┤ļĪĀ zT ņĄ£ļīĆĻ░ÆņØĆ Zhou et al.ņØ┤ ļ│┤Ļ│ĀĒĢ£ x= 0.08 ņāśĒöīņØś zT ņĖĪņĀĢĻ░Æ (zT = 0.160) ļīĆļ╣ä ņĢĮ 2.2ļ░░ ļåÆņĢśļŗż. SPB ļ¬©ļŹĖņŚÉ ļö░ļź┤ļ®┤ ĻĖ░ņĪ┤ x= 0.08 ņāśĒöīņØś nHļź╝ 9.06 ├Ś 1018 cm-3ļĪ£ ĒŖ£ļŗØĒĢĀ Ļ▓ĮņÜ░, ņØ┤ļĪĀņĀüņ£╝ļĪ£ ņśłņĖĪĒĢ£ zT = 0.311ņØä 300 KņŚÉņä£ ļÅäļŗ¼ĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆĒĢ£ļŗż.
AcknowledgmentsThis work was supported by the Basic Study and Interdisciplinary R&D Foundation Fund of the University of Seoul (2022) for Hyun-Sik Kim. This work was also financially supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2019R1A6A1A11055660, NRF2015R1A6A1A03031833) for Won-Seon Seo and Heesun Yang. This work was also supported by the Technology Innovation Program RS-2022-00154720 funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea) for Weon Ho Shin.
Fig.┬Ā1.(a) Experimental (symbols from Ref. 26) and calculated (lines) S as a function of nH for Sn1-xBixTe (x = 0 - 0.08) at 300 K. (b) The md* calculated as a function of Bi doping content (x). (c) Experimental (symbols from Ref. 26) and calculated (lines) ╬╝H as a function of nH for different x. (d) The ╬╝0 calculated as a function of x. 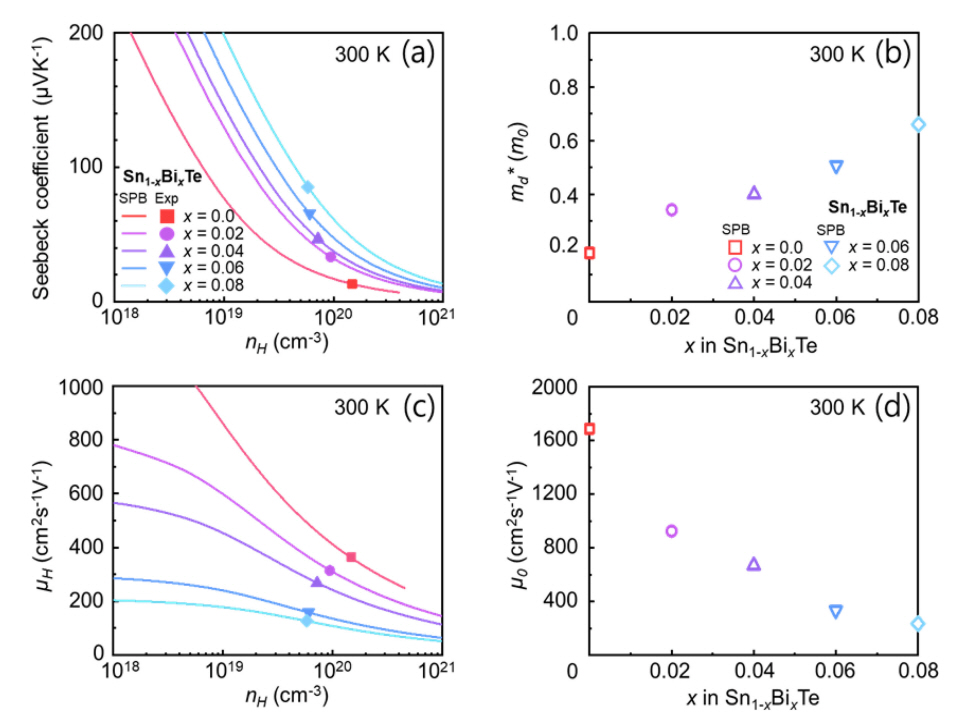
Fig.┬Ā2.(a) Experimental (symbols from Ref. 26) and calculated (lines) Žā as a function of nH for Sn1-xBixTe (x = 0 - 0.08) at 300 K. (b) The theoretical Žā calculated as a function of Bi doping content (x). (c) Calculated (lines) L as a function of nH for different x. (d) The L calculated as a function of x. (e) Experimental (symbols from Ref. 26) and calculated (lines) ╬║e as a function of nH for Sn1-xBixTe (x = 0 - 0.08) at 300 K. (f) Calculated ╬║e as a function of x. 
Fig.┬Ā3.(a) Weighted mobility(╬╝w) of Sn1-xBixTe(x = 0 - 0.08) calculated as a function of x at 300 K. (b) Experimental (symbols from Ref. 26) and calculated (lines) Power factor (PF) as a function of nH for different x. (c) B-factor calculated as a function of x. (d) Lattice thermal conductivity (╬║l) calculated as a function of x. 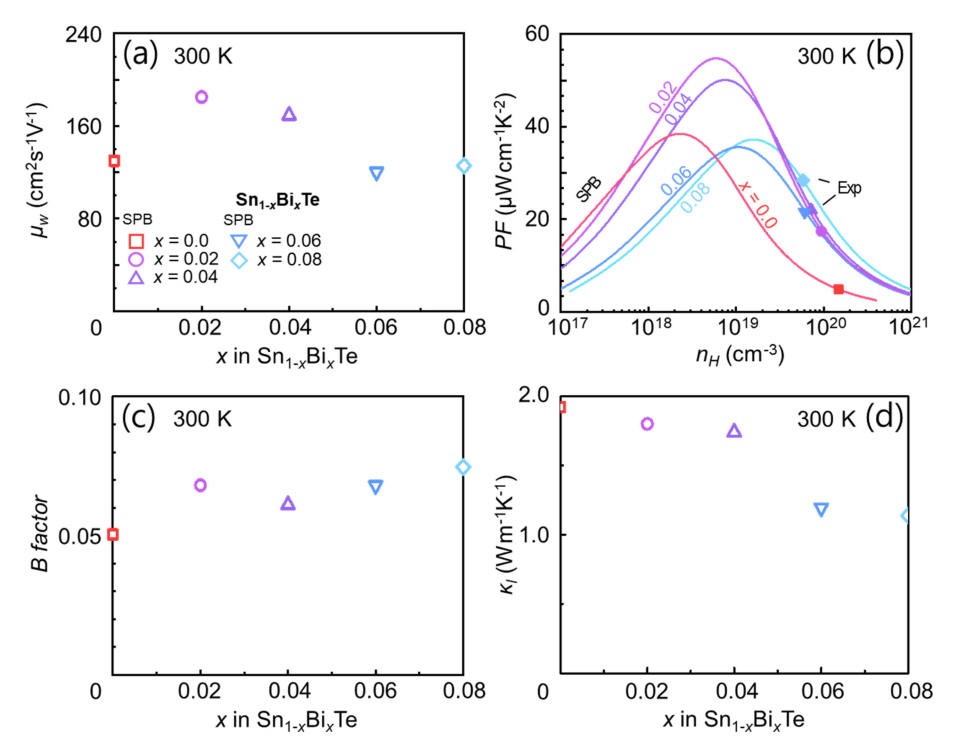
REFERENCES1. S. Rahimifrad and H. Trollman, Int. J. Sustain. Eng. 11, 1 (2018).
3. G. J. M. Velders, A. R. Ravishankara, M. K. Miller, M. J. Molina, J. Alcamo, M. J. Daniel, D. W. Fahey, S. A. Montzka, and S. Reimann, Science. 335, 922 (2012).
5. G. Tan, M. Ohta, and M. G. Kanatzidis, Philos. Trans. R. Soc. London Ser. A. 377, 20180450 (2019).
9. H. Kim, N. A. Heinz, Z. M. Gibbs, Y. Tang, S. D. Kang, and G. J. Snyder, Mater. Today. 20, 452 (2019).
10. M. Heo, S.-H. Kwon, S.-i. Kim, H. Park, K.-H. Lee, and H.-S. Kim, J. Alloys Compd. 954, 170144 (2023).
12. G. Tang, L. Zhao, F. Shi, J. W. Doak, S. Lo, H. Sun, C. Wolverton, V. P. Dravid, C. Uher, and M. G. Kanatzidis, J. Am. Chem. Soc. 136, 7006 (2014).
15. Q. Zhang, B. Liao, Y. Lan, K. Lukas, W. Liu, K. Esfarjani, C. Opeil, D. Broido, G. Chen, and Z. Ren, Proc. Natl. Acad. Sci. U. S. A. 110, 13261 (2013).
16. G. Tan, F. Shi, S. Hao, H. Chi, T. P. Bailey, L. Zhao, C. Uher, C. Wolverton, V. P. Dravid, and M. G. Kanatzidis, J. Am. Chem. Soc. 137, 5100 (2015).
18. H. Wu, C. Chang, D. Feng, Y. Xiao, X. Zhang, Y. Pei, L. Zheng, D. Wu, S. Gong, Y. Chen, J. He, M. G. Kanatzidis, and L. Zhao, Energy Environ. Sci. 8, 267 (2015).
19. J. Nishitani, K. M. Yu, and W. Walukiewicz, Appl. Phys. Lett. 105, 132103 (2014).
20. J. He, J. Xu, G. Liu, H. Shao, X. Tan, Z. Liu, J. Xu, H. Jiang, and J. Jiang, RSC Adv. 6, 32189 (2016).
21. M. Novak, S. Sasaki, M. Kriener, K. Segawa, and Y. Ando, Phys. Rev. B. 88, 140502 (2013).
22. G. Tan, W. G. Zeier, F. Shi, P. Wang, G. J. Snyder, V. P. Dravid, and M. G. Kanatzidis, Chem. Mater. 27, 7801 (2015).
23. L. Zhao, X. Zhang, H. Wu, G. Tan, Y. Pei, Y. Xiao, C. Chang, D. Wu, H. Chi, L. Zheng, S. Gong, C. Uher, J. He, and M. G. Kanatzidis, J. Am. Chem. Soc. 138, 2366 (2016).
24. T. Liang, X. Su, X. Tan, G. Zheng, X. She, Y. Yan, X. Tang, and C. Uherb, J. Mater. Chem. C. 3, 8550 (2015).
25. G. Tan, F. Shi, H. Sun, L. Zhao, C. Uher, V. P. Dravid, and M. G. Kanatzidis, J. Mater. Chem. A. 2, 20849 (2014).
26. Z. Zhou, J. Yang, Q. Jiang, Y. Luo, D. Zhang, Y. Ren, X. He, and J. Xin, J. Mater. Chem. A. 4, 13171 (2016).
29. G. J. Snyder, A. H. Snyder, M. Wood, R. Gurunathan, B. H. Snyder, and C. Niu, Adv. Mater. 32, 2001537 (2020).
|
|
|||||||||||||||||||||||||||||||||||||||