1. ņä£ ļĪĀ
RF-ID (Radio Frequency IDentification)ļ×Ć ņĀäĒīīļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņøÉĻ▒░ļ”¼ņŚÉ ņĀĢļ│┤ļź╝ ņØĖņŗØĒĢśļŖö ĻĖ░ņłĀņØ┤ļŗż. RF-ID ĻĖ░ņłĀņØĆ RF-ID Ēā£ĻĘĖņØś ņ¦æņĀüĒÜīļĪ£ņŚÉ ņĀĢļ│┤ļź╝ ĻĖ░ļĪØĒĢśĻ│Ā, ņĢłĒģīļéśļź╝ ĒåĄĒĢ┤ RF-ID ĒīÉļÅģĻĖ░ņŚÉ ņĀĢļ│┤ļź╝ ņåĪņŗĀĒĢśļŖö ļ░®ņŗØņ£╝ļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦äļŗż. RF-ID Ēā£ĻĘĖņØś ņóģļźśļŖö ļ░░Ēä░ļ”¼ņØś ņ£Āļ¼┤ņŚÉ ļö░ļØ╝ ļŖźļÅÖĒśĢ Ēā£ĻĘĖņÖĆ ņłśļÅÖĒśĢ Ēā£ĻĘĖļĪ£ ļČäļźśĒĢśļ®░, ņĀäĒīīņØś ņŻ╝Ēīīņłś ļīĆņŚŁņŚÉ ļö░ļØ╝ ņĀĆņŻ╝Ēīī, Ļ│ĀņŻ╝Ēīī, ņ┤łĻ│ĀņŻ╝Ēīī, ļ¦łņØ┤Ēü¼ļĪ£Ēīī ļīĆņŚŁņ£╝ļĪ£ ļČäļźśĒĢ£ļŗż [1,2]. RF-IDļŖö ļ░öņĮöļō£ļź╝ ļīĆņ▓┤ĒĢśļ®┤ņä£ ņ£ĀĒåĄ/ļ¼╝ļźś ņŚģĻ│äņŚÉņä£ ĒÖ£ņÜ®ņØ┤ ņ”ØļīĆĒĢśĻ│Ā ņ׳ņ£╝ļ®░, Ē¢źĒøä UHF (868~960 MHz)ļéś ļ¦łņØ┤Ēü¼ļĪ£Ēīī (2.45 GHz)ņØś ņŻ╝Ēīīņłśļź╝ ņé¼ņÜ®ĒĢ£ļŗż.
ņØ┤ņ▓śļ¤╝ RF-ID ĻĖ░ņłĀņØĆ Ļ░£ļ│ä ņĢäņØ┤Ēģ£ņØś ņŗØļ│äņØ┤ Ļ░ĆļŖźĒĢśĻ│Ā, ņØĖņŗØ Ļ▒░ļ”¼Ļ░Ć ĻĖĖļ®░, ļŗżņ¢æĒĢ£ Ēā£ĻĘĖ ĒÅ╝ņØä Ļ░Ćņ¦ł ņłś ņ׳ņØä ļ┐Éļ¦ī ņĢäļŗłļØ╝, Ēā£ĻĘĖņØś ņ×¼ĻĖ░ļĪØņØ┤ Ļ░ĆļŖźĒĢśņŚ¼ ņāüļŗ╣Ē׳ ņ£ĀņÜ®ĒĢ£ ņןņĀÉņØä Ļ░Ćņ¦ĆĻ│Ā ņ׳ļŗż. ļ░śļ®┤ņŚÉ Ļ│ĀĻ░ĆņØś Ēā£ĻĘĖ Ļ░ĆĻ▓®Ļ│╝ ĻĖłņåŹ ļō▒ ņŻ╝ļ│Ć ĒÖśĻ▓ĮņŚÉ ļ»╝Ļ░ÉĒĢśĻ▓ī ņśüĒ¢źņØä ļ░øļŖö ņĀÉņØĆ ļŗ©ņĀÉņ£╝ļĪ£ ņ¦ĆņĀüļÉśĻ│Ā ņ׳ļŗż [3,4]. Reader, writer ņŻ╝ļ│ĆņŚÉ ĻĖłņåŹĒīÉņØ┤ ņ׳ņ£╝ļ®┤ ĻĘĖ ļ░śņé¼ļĪ£ ņØĖĒĢ┤ RF-ID ņŗĀĒśĖļź╝ ņĀ£ļīĆļĪ£ ņØĮņ¢┤ ļōżņØ┤ņ¦Ć ļ¬╗ĒĢśļŖö ļ¼ĖņĀ£Ļ░Ć ļ░£ņāØĒĢĀ ņłś ņ׳ļŗż. RF-ID ņŗ£ņŖżĒģ£ņØ┤ ĻĄ¼ņČĢļÉ£ ņןņåīņŚÉ ņŚ¼ļ¤¼ Ļ░£ņØś RF-IDĻ░Ć ņ׳ņØä Ļ▓ĮņÜ░ ņāüĒśĖ Ļ░äņäŁņ£╝ļĪ£ ņØĖĒĢ£ Ēā£ĻĘĖ ņĀĢļ│┤ņØś ļłäļØĮņØ┤ ļŹöņÜ▒ ņŗ¼Ļ░üĒĢ┤ņ¦ł ņłś ņ׳ļŗż. ļśÉĒĢ£ ļ¬©ļ░öņØ╝ RF-IDĻ░Ć ņāüņÜ®ĒÖöļÉśņŚłņØä Ļ▓ĮņÜ░, ļÅÖņØ╝ Ļ│ĄĻ░äņŚÉņä£ ņé¼ņÜ®ļÉśļŖö readerņØś ņł½ņ×ÉĻ░Ć ļŖśņ¢┤ļéśĻ▓ī ļÉśļ®┤ reader Ļ░ä Ļ░äņäŁņØ┤ ļŹö ņŗ¼Ļ░üĒĢ┤ņ¦ł Ļ▓āņ£╝ļĪ£ ņśłņāüļÉ£ļŗż. ņØ┤ ļĢīļ¼ĖņŚÉ RF-ID ņŗ£ņŖżĒģ£ņŚÉņä£ ņĀäņ×ÉĒīī Ļ░äņäŁņØä ņżäņØ┤Ļ│Ā ņØĖņŗØļźĀņØä ļåÆņØ┤ĻĖ░ ņ£äĒĢ£ ņĀäņ×ÉĒīī ņןĒĢ┤ ļīĆņ▒ģ ĻĖ░ņłĀņØ┤ ĒĢäņÜöĒĢśļŗż [5-9]. ņØ┤ļ¤¼ĒĢ£ ļ¼ĖņĀ£ ĒĢ┤Ļ▓░ ļ░®ņĢłņ£╝ļĪ£ ņĀäņ×ÉĒīī ĒØĪņłś sheet ļśÉļŖö ĒīÉļä¼ ņĀ£ĒÆłņØś ņé¼ņÜ®ņØä Ļ▓ĆĒåĀĒĢĀ ņłś ņ׳ļŗż.
ņĀäņ×ÉĒīī ĒØĪņłśņ×¼ļŻīļĪ£ ņé¼ņÜ®ļÉśļŖö ņŻ╝ļÉ£ ņåīņ×¼ļŖö ĒÄśļØ╝ņØ┤ĒŖĖ ļśÉļŖö ņ▓ĀĻ│ä ĻĖłņåŹĻ│╝ Ļ░ÖņØĆ ņŚ░ņ×Éņä▒ ņ×¼ļŻīņØ┤ļŗż [10-18]. ņØ┤ ņżæņŚÉņä£ ņĀäņ×ÉĒīī ĒØĪņłśņ×¼ļŻīļĪ£ ĒÄśļØ╝ņØ┤ĒŖĖ ņ×Éņä▒ņ▓┤ļź╝ ņé¼ņÜ®ĒĢśļŖö ņØ┤ņ£ĀļŖö ļåÆņØĆ ņ×ÉĻĖ░ņåÉņŗż ĒŖ╣ņä▒ņŚÉ ĻĘ╝Ļ▒░ĒĢśĻ│Ā, ņ×¼ļŻīņØś ĒÖöĒĢÖņĪ░ņä▒ņØä ļ│ĆĒÖöņŗ£ņ╝£ ņé¼ņÜ® ņŻ╝Ēīīņłś ļīĆņŚŁņØä ņĀ£ņ¢┤ĒĢĀ ņłś ņ׳ĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ņØ╝ļ░śņĀüņ£╝ļĪ£ ņŖżĒö╝ļä¼Ļ│ä ĒÄśļØ╝ņØ┤ĒŖĖļŖö 1 GHz ļ»Ėļ¦īņØś ļīĆņŚŁņŚÉņä£ ļīĆļČĆļČä ņ×ÉņŚ░Ļ│Ąļ¬ģņŻ╝ĒīīņłśĻ░Ć ļéśĒāĆļéś 0.5~2.5 GHz ļīĆņŚŁņŚÉņä£ ŌĆō20 dB ņØ┤ĒĢśņØś ņ¢æĒśĖĒĢ£ ņĀäĒīīĒØĪņłśĒŖ╣ņä▒ņØä ļéśĒāĆļé┤ņ¦Ćļ¦ī, ļæÉĻ╗śĻ░Ć 5 mm ņØ┤ņāüņ£╝ļĪ£ ļæÉĻ║╝ņøīņ¦ĆļŖö ļŗ©ņĀÉņØ┤ ņ׳ļŗż [10,11]. ņä╝ļŹöņŖżĒŖĖ ļČäļ¦ÉĻ│╝ Ļ░ÖņØĆ Ļ│ĀĒł¼ņ×Éņ£© ņ▓ĀĻ│ä ņŚ░ņ×Éņä▒ ņ×¼ļŻīļź╝ ņé¼ņÜ®ĒĢśņŚ¼ 1-2 GHz ļīĆņŚŁņÜ® ļģĖņØ┤ņ”ł ĒØĪņłś ļśÉļŖö ņĀäņ×ÉĒīī ĒØĪņłś sheetĻ░Ć Ļ░£ļ░£ļÉśņŚłņ£╝ļéś, 1 GHz ņØ┤ĒĢśņØś UHF ļīĆņŚŁņŚÉņä£ļŖö ĒØĪņłś ņä▒ļŖźņØ┤ ļ¢©ņ¢┤ņ¦ĆĻ│Ā ĒÄśļØ╝ņØ┤ĒŖĖņÖĆ ļ¦łņ░¼Ļ░Ćņ¦ĆļĪ£ ļæÉĻ╗ś ļ░Å ļ¼┤Ļ▓īĻ░Ć ņ”ØĻ░ĆĒĢśļŖö ļŗ©ņĀÉņØ┤ ņ׳ļŗż [13-16].
ņØ┤ļ¤¼ĒĢ£ ļ¼ĖņĀ£ņØś ĒĢ┤Ļ▓░ ļ░®ņĢłņ£╝ļĪ£ ļ®öĒāĆņåīņ×¼ņØś ļÅäņ×ģņØä Ļ▓ĆĒåĀĒĢĀ ņłś ņ׳ļŗż. ļ®öĒāĆņåīņ×¼ļŖö ņØĖĻ│ĄņĀüņØĖ ļÅäņ▓┤ Ēī©Ēä┤ņØś ĻĄ¼ņä▒ ņÜöņåīļź╝ ņ£ĀņĀäņ▓┤ ĻĖ░ĒīÉ ņ£äņŚÉ ņŻ╝ĻĖ░ņĀüņ£╝ļĪ£ ļ░░ņ╣śĒĢśņŚ¼ ņĀ£ņ×æļÉ£ ņ×¼ļŻīļź╝ ņ╣ŁĒĢśļŖö Ļ▓āņ£╝ļĪ£, ļŗ©ņ£ä ņģĆņØś Ēü¼ĻĖ░Ļ░Ć ļ¼╝ņ¦ł ņ×Éņ▓┤ņØś ļČäņ×É Ēü¼ĻĖ░ļ│┤ļŗżļŖö Ēø©ņö¼ ņ╗żņä£ Ļ▒░ņŗ£ņĀü ļ¦źņŖżņø░ ļ░®ņĀĢņŗØņØś ņĀüņÜ®ņØ┤ ĒāĆļŗ╣ĒĢśĻ│Ā, ņĀäņ×ÉĒīīņØś Ēīīņןļ│┤ļŗżļŖö Ēü¼ĻĖ░Ļ░Ć ļ¦żņÜ░ ņ×æņĢä ņ£ĀĒÜ©ļ¦żņ¦łņØ┤ļĪĀņØś ņĀüņÜ®ņØ┤ Ļ░ĆļŖźĒĢ£ mesoscopic ņŖżņ╝ĆņØ╝ņØś ĻĄ¼ņĪ░ļź╝ ņØ╝ņ╗½ļŖöļŗż [19,20]. ņ×ÉĻĖ░ņĀü ĒŖ╣ņä▒ņØä ņĀ£ņ¢┤ĒĢśļŖö split ring resonator (SRR)ņÖĆ ņĀäĻĖ░ņĀü ĒŖ╣ņä▒ņØä ņĪ░ņĀłĒĢśļŖö strip dipole (SD)ņØ┤ ļīĆĒæ£ņĀüņ£╝ļĪ£ ņĀ£ņĢłļÉ£ ļÅäņ▓┤ Ēī©Ēä┤ņØ┤ļŗż [21-23]. ņØ┤ļ¤¼ĒĢ£ ĻĄ¼ņĪ░ļź╝ ņØ┤ņÜ®ĒĢ£ ļ®öĒāĆņåīņ×¼ ĒØĪņłśņ▓┤ļŖö ring resonatorņÖĆ ĻĖłņåŹ ņäĀņØś ņØĖļŹĢĒä┤ņŖż (L) ļ░Å ņ╗żĒī©ņŗ£Ēä┤ņŖż (C), ĻĘĖļ”¼Ļ│Ā ņØ┤ļōż Ļ░äņØś ņ╗żĒöīļ¦üņŚÉ ņØśĒĢ┤ Ēł¼ņ×Éņ£©, ņ£ĀņĀäņ£©ņØä ņĀ£ņ¢┤ĒĢśļŖö ņøÉļ”¼ņŚÉ ĻĘ╝Ļ▒░ĒĢ£ļŗż [24,25]. ļö░ļØ╝ņä£ ĻĖ░ĒīÉ ļæÉĻ╗śņŚÉ ļīĆĒĢ£ ņĀ£ņĢĮņØ┤ ņĀüĻ│Ā (ļ░ĢĒśĢĒÖö), ņØĖĻ│ĄņĀüņØĖ ĻĄ¼ņĪ░ (ļŗ©ņ£ä ņģĆņØś ĻĄ¼ņĪ░ ļ░Å Ēü¼ĻĖ░) ņĪ░ņĀłņŚÉ ņØśĒĢ┤ ļŗżņżæļ░┤ļō£ ĒØĪņłś ĒŖ╣ņä▒ņØä ņ¢╗ņØä ņłś ņ׳ļŖö ņןņĀÉņØ┤ ņ׳ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļ®öĒāĆņåīņ×¼ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ RF-IDņØś ņĀäņ×ÉĒīī Ļ░äņäŁ ļīĆņ▒ģņÜ® ņĀäĒīīĒØĪņłśņ▓┤ļź╝ ņäżĻ│äĒĢśņśĆļŗż. ļ░░ļ®┤ņØ┤ ĻĖłņåŹņ£╝ļĪ£ ļŗ©ļØĮļÉ£ ņ£ĀņĀäņ▓┤ ĻĖ░ĒīÉ ņ£äņŚÉ ĻĘĖļ”¼ļō£ Ēī©Ēä┤ņØś ļÅäņ▓┤ļź╝ ļ░░ņŚ┤ĒĢśņŚ¼ 0.8 GHz ļīĆņÖĆ 2.4 GHz ļīĆņØś ņØ┤ņżæ ņŻ╝Ēīīņłś ļīĆņŚŁņŚÉņä£ ŌĆō10 dB ņØ┤ĒĢśņØś ļ░śņé¼ņåÉņŗżņØä ļ│┤ņØ┤ļ®░, ļæÉĻ╗śĻ░Ć 3-4 mm ņłśņżĆņØĖ ļ░ĢĒśĢņØś ņĀäĒīīĒØĪņłśņ▓┤ļź╝ ņĀ£ņĢłĒĢśņśĆļŗż.
2. ņŗ£ļ«¼ļĀłņØ┤ņģś ļ¬©ļŹĖ
ĻĘĖļ”╝ 1ņØĆ ĻĘĖļ”¼ļō£ Ēī©Ēä┤ņØś ļ®öĒāĆņåīņ×¼ ĒØĪņłśņ▓┤ (grid-pattern metamaterial absorbers: GPMA)ņØś ļŗ©ņ£ä ņģĆ ĻĄ¼ņĪ░ļÅäņØ┤ļŗż. GPMAļŖö ĻĘĖļ”╝ 1(a)ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ļ░░ļ®┤ņØ┤ ļÅäņ▓┤ļĪ£ ļŗ©ļØĮļÉ£ ņ£ĀņĀäņ▓┤ ĻĖ░ĒīÉ ņ£äņŚÉ ĻĘĖļ”¼ļō£ ĒśĢĒā£ņØś ļÅäņ▓┤ Ēī©ņ╣śĻ░Ć ņŻ╝ĻĖ░ņĀüņ£╝ļĪ£ ļ░░ņŚ┤ļÉ£ ĻĄ¼ņĪ░ļź╝ ņĘ©ĒĢ£ļŗż. ļŗ©ņ£ä ņģĆ ļ░Å ĻĘĖļ”¼ļō£ ļÅäņ▓┤ņØś Ēü¼ĻĖ░ļŖö ĻĘĖļ”╝ 1(b)ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ņŻ╝ņ¢┤ņ¦äļŗż. ļŗ©ņ£ä ņģĆņØś ņŻ╝ĻĖ░ (p = 95 ~ 100 mm), ļÅäņ▓┤ņØś ĻĖĖņØ┤ (l = 65 ~ 73 mm) ļ░Å ĒÅŁ (w1 = 8.8 ~ 9.0 mm, w2 = 4.5 ~ 5.0 mm), ĻĘĖļ”¼Ļ│Ā ļÅäņ▓┤ņØś ļæÉĻ╗ś(tm = 0.015 ~ 0.02 mm)ļź╝ ļ│ĆĒÖöņŗ£Ēéżļ®┤ņä£ ļ░śņé¼ņåÉņŗżņØä ņŗ£ļ«¼ļĀłņØ┤ņģśĒĢśņśĆļŗż. ņāüņÜ®ņØś ņŗ£ļ«¼ļĀłņØ┤ņģś Ēł┤ņØĖ Ansoft ņé¼ņØś HFSS 13.0ņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ņé¼ņÜ®ĒĢ£ ņ£ĀņĀäņ▓┤ ĻĖ░ĒīÉņØĆ FR4ļĪ£ ļ│Ąņåīņ£ĀņĀäņ£©ņØĆ ╬Ąr = 4.1 + j0.03ņ£╝ļĪ£ ņŻ╝ņ¢┤ņ¦ĆĻ│Ā, ļæÉĻ╗śļŖö ts = 3.25 ~ 3.75 mmņØ┤ļŗż. ĻĖłņåŹ ļÅäņ▓┤ļŖö ĻĄ¼ļ”¼ (ņĀäĻĖ░ņĀäļÅäļÅä = 5.8 ├Ś 107 S/m)ņØ┤ļŗż.
3. Ļ▓░Ļ│╝ ļ░Å Ļ│Āņ░░
3.1. ļ░śņé¼ņåÉņŗż
RF-IDņØś ļÅÖņ×æ ņŻ╝ĒīīņłśņØĖ 0.8 GHz ļīĆņÖĆ 2.4 GHz ļīĆņŚÉņä£ ļ¬©ļæÉ ņé¼ņÜ® Ļ░ĆļŖźĒĢ£ GPMAņØś ņĄ£ņĀü ņäżĻ│äļź╝ HFSS ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ĒåĄĒĢśņŚ¼ ļÅäņČ£ĒĢśņśĆļŗż. ļŗ©ņ£ä ņģĆ ļ░Å ĻĘĖļ”¼ļō£ ļÅäņ▓┤ņØś Ēü¼ĻĖ░ļź╝ Ēæ£ 1ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ļ│ĆĒÖöņŗ£ņ╝░ņØä ļĢī, ņ╣śņłś D (p = 100 mm, l = 73 mm, w1 = 9.0 mm, w2 = 4.5 mm, ts = 3.75 mm, tm = 0.015 mm)ņŚÉņä£ Ļ░Ćņן ņóŗņØĆ Ļ▓░Ļ│╝ļź╝ ņ¢╗ņØä ņłś ņ׳ņŚłĻ│Ā, ĻĘĖ Ļ▓░Ļ│╝ļź╝ ĻĘĖļ”╝ 2ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. f1= 0.88 GHzņŚÉņä£ ŌĆō12 dB, f2 = 2.48 GHzņŚÉņä£ ŌĆō15 dBņØś ļ░śņé¼ņåÉņŗżņØä ļ│┤ņØĖļŗż. ļŗ©ņ£ä ņģĆņØś Ēü¼ĻĖ░ļź╝ p = 95mmļĪ£ ņżäņśĆņØä Ļ▓ĮņÜ░ (ņ╣śņłś A), ņŻ╝Ēīīņłś ļīĆņŚŁņØ┤ Ļ░üĻ░ü f1 = 1.0 GHz, f2 = 2.78 GHzļĪ£ ņ”ØĻ░ĆĒĢśņŚ¼ ļ¬®Ēæ£ ņŻ╝Ēīīņłś ļīĆņŚŁņŚÉņä£ ļ▓Śņ¢┤ļé£ļŗż. ĻĖ░ĒīÉņØś ļæÉĻ╗śĻ░Ć ts= 3.25 ~ 3.50 mmļĪ£ ņ×æņØĆ Ļ▓ĮņÜ░ (ņ╣śņłś B, C), ļ░śņé¼ņåÉņŗżņØ┤ ņĢĮĻ░ä ņ”ØĻ░ĆĒĢśņŚ¼ ņĄ£ņĀü ņäżĻ│äņŚÉņä£ ļ▓Śņ¢┤ļé£ļŗż. ĻĘĖļ”¼ļō£ ļÅäņ▓┤ņØś ļæÉĻ╗śļź╝ tm = 0.02 mmļĪ£ ņ”ØĻ░Ćņŗ£ņ╝░ņØä Ļ▓ĮņÜ░ņŚÉļÅä (ņ╣śņłś E), ļ░śņé¼ņåÉņŗżņØ┤ ņ”ØĻ░ĆĒĢśļŖö Ļ▓ĮĒ¢źņØä ļ│┤ņØĖļŗż.
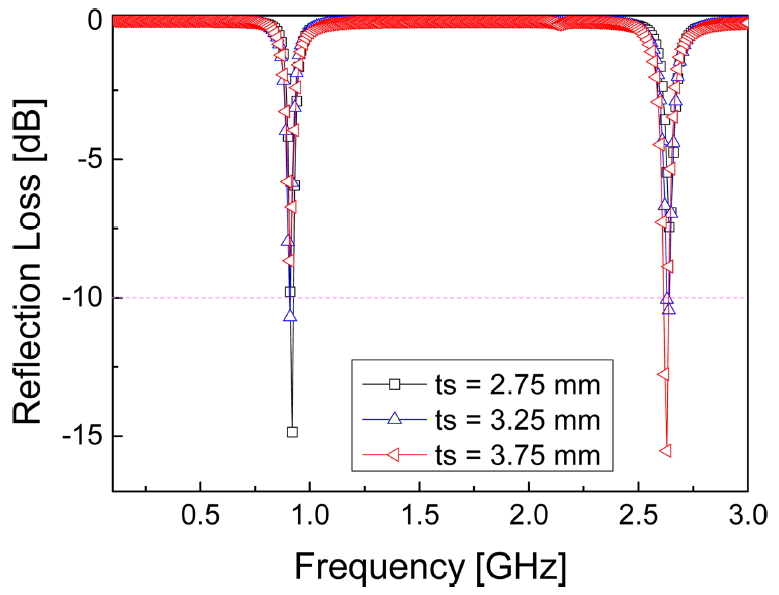
ņāüĻĖ░ ņĄ£ņĀü ņäżĻ│äņ╣ś (ĻĘĖļ”╝ 2)ļŖö GPMA ĒīīļØ╝ļ»ĖĒä░ Ļ░üĻ░üņŚÉ ļīĆĒĢ┤ ņ╣śņłś ļ│ĆĒÖöņŚÉ ļö░ļźĖ ļ░śņé¼ņåÉņŗżņØä ņŗ£ļ«¼ļĀłņØ┤ņģś ĒĢśņŚ¼ ņ¢╗ņ¢┤ņ¦ä Ļ▓░Ļ│╝ņØ┤ļŗż. ņØ╝ļĪĆļĪ£ ĻĘĖļ”╝ 3ņØĆ GPMAņØś ņ╣śņłśĻ░Ć ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ņŻ╝ņ¢┤ņ¦ĆĻ│Ā (p = 86.5 mm, l = 70 mm, tm = 0.02 mm, w1 = 4.4 mm, w2 = 8.8 mm), ņ£ĀņĀäņ▓┤ ĻĖ░ĒīÉņØś ļæÉĻ╗śļź╝ ts = 2.75, 3.25, 3.75 mmļĪ£ ļ│ĆĒÖöņŗ£ņ╝░ņØä ļĢī, HFSS ņāüņÜ® Ēł┤ņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņŗ£ļ«¼ļĀłņØ┤ņģśĒĢ£ ļ░śņé¼ņåÉņŗż ĻĘĖļלĒöäņØ┤ļŗż. 0.91 GHz ņÖĆ 2.64 GHzņŚÉņä£ ļ░śņé¼ņåÉņŗżņØ┤ ņĄ£ņåīĻ░Ć ļÉśļŖö ņØ┤ņżæļ░┤ļō£ ĒØĪņłśĒŖ╣ņä▒ņØä ļ│┤ņØĖļŗż. ņ£ĀņĀäņĖĄņØś ļæÉĻ╗śĻ░Ć ņ”ØĻ░ĆĒĢśļ®┤ņä£ 0.91 GHzņŚÉņä£ļŖö ļ░śņé¼ņåÉņŗż ņ¢æņØ┤ ņĀÉņ░© ņ”ØĻ░ĆĒĢśņśĆĻ│Ā, 2.64 GHzņŚÉņä£ļŖö ļæÉĻ╗śĻ░Ć ņ”ØĻ░ĆĒĢĀņłśļĪØ ļ░śņé¼ņåÉņŗż ņ¢æņØ┤ ņĀÉņ░© Ļ░ÉņåīĒĢśņśĆļŗż (Ēæ£ 2 ņ░ĖņĪ░). ļ░śņé¼ņåÉņŗż ŌĆō10 dBļź╝ ĻĖ░ņżĆĒĢśņśĆņØä ļĢī, ņ£ĀņĀäņ▓┤ņØś ļæÉĻ╗śĻ░Ć 3.25 mmņØ╝ ļĢī ņØ┤ ņĪ░Ļ▒┤ņŚÉ Ļ░Ćņן ļ¦īņĪ▒ĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ļŗżļźĖ ĒīīļØ╝ļ»ĖĒä░ņŚÉ ļīĆĒĢ┤ņä£ļÅä ņØ┤ņÖĆ Ļ░ÖņØĆ ņĄ£ņĀüĒÖö ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņłśĒ¢ēĒĢśņśĆļŗż.
3.2. ņĀäļźśļ░ĆļÅä ļČäĒż
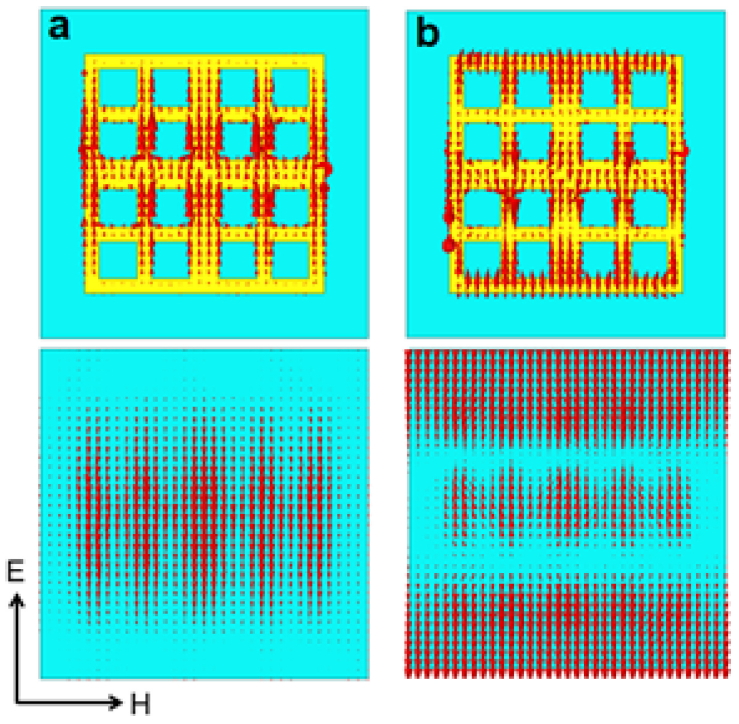
ĻĘĖļ”╝ 4ļŖö ņĄ£ļīĆ ĒØĪņłś ņŻ╝Ēīīņłś (0.88 GHz, 2.48 GHz)ņŚÉņä£ ĻĘĖļ”¼ļō£ ļÅäņ▓┤ņÖĆ ļ░░ļ®┤ ņĀæņ¦Ć ļÅäņ▓┤ņŚÉ ņ£ĀĻĖ░ļÉ£ ņĀäļźśļ░ĆļÅä ļČäĒżļź╝ ļ│┤ņŚ¼ņżĆļŗż. ņ▓½ņ¦Ė Ēö╝Ēü¼Ļ░Ć ļéśĒāĆļéśļŖö 0.88 GHzņŚÉņä£ļŖö ĻĘĖļ”¼ļō£ ļÅäņ▓┤ņØś ņżæņĢÖņŚÉņä£ ņĀäļźśĻ░Ć Ļ░ĢĒĢśĻ▓ī ĒØÉļź┤Ļ│Ā ņ׳Ļ│Ā, ļ░░ļ®┤ ņĀæņ¦Ćļ®┤ņŚÉņä£ļŖö ņĀäļ®┤ ĻĘĖļ”¼ļō£ ļÅäņ▓┤ ĒØÉļź┤ļŖö ņĀäļźśņØś ļ░®Ē¢źĻ│╝ ļ░śļīĆ ļ░®Ē¢źņØś ņĀäļźśĻ░Ć ļČäĒżļÉśņ¢┤ ņÖĖļČĆ ņ×ÉĻ│äņŚÉ ļīĆĒĢ£ ņ×ÉĻĖ░ ļ░śņØæņØä ļ│┤ņØĖļŗż. ļö░ļØ╝ņä£ 0.88 GHzņŚÉņä£ņØś Ļ│Ąņ¦äņØĆ ņ×ÉĻĖ░ Ļ│Ąņ¦äņØ┤ļ®░, Ļ│Ąņ¦äņŻ╝ĒīīņłśņŚÉņä£ Lorentz ĒśĢņØś Ēł¼ņ×Éņ£© ņŖżĒÄÖĒŖĖļ¤╝ņØä ļ│┤ņØĖļŗż. ļö░ļØ╝ņä£ ĻĘĖļ”¼ļō£ ļÅäņ▓┤ŌłÆļ░░ļ®┤ ņĀæņ¦Ć ļÅäņ▓┤ ņīŹņØĆ ĒĢśļéśņØś ņ×ÉĻĖ░Ļ│Ąņ¦äĻĖ░ļĪ£ ņĘ©ĻĖēļÉĀ ņłś ņ׳ļŗż(ĻĘĖļ”╝ 4(a)). ļæśņ¦Ė ĒØĪņłś Ēö╝Ēü¼Ļ░Ć ļéśĒāĆļéśļŖö 2.48 GHzņŚÉņä£ļŖö ĻĘĖļ”¼ļō£ ļÅäņ▓┤ņØś ņāü, ņżæ, ĒĢśņŚÉņä£ ņä£ļĪ£ ļ░śļīĆ ļ░®Ē¢źņØś ņĀäļźśĻ░Ć ĒØÉļź┤Ļ│Ā ņ׳ļŗż (ĻĘĖļ”╝ 4(b)). ļ░░ļ®┤ņØś ņĀæņ¦Ćļ®┤ņŚÉņä£ļŖö ņāü, ņżæ, ĒĢś ļČĆļČäņŚÉņä£ ĻĘĖļ”¼ļō£ ļÅäņ▓┤ņÖĆļŖö ņä£ļĪ£ ļ░śļīĆ ļ░®Ē¢źņ£╝ļĪ£ ņĀäļźśĻ░Ć ĒØśļ¤¼ ņÖĖļČĆ ņ×ÉĻ│äņŚÉ ļīĆĒĢ£ ņ×ÉĻĖ░Ļ│Ąņ¦ä ļ░śņØæņØä ļ│┤ņØĖļŗż. ļö░ļØ╝ņä£ 2.48 GHzņŚÉņä£ļŖö 3Ļ░£ņØś ņ×ÉĻĖ░Ļ│Ąņ¦äĻĖ░Ļ░Ć ņĪ┤ņ×¼ĒĢ£ļŗżĻ│Ā ļ│╝ ņłś ņ׳ļŗż. Ļ│Ąņ¦äĻĖ░ņØś Ēü¼ĻĖ░Ļ░Ć ļīĆļץ 1/3ļĪ£ ņżäĻĖ░ ļĢīļ¼ĖņŚÉ, Ļ│Ąņ¦äņŻ╝ĒīīņłśļŖö ņĢĮ 3ļ░░ļĪ£ ņ”ØĻ░ĆĒĢ£ļŗż. ĻĖłņåŹ ĻĄ¼ņĪ░ļ¼╝ņŚÉņä£ ļéśĒāĆļéśļŖö 1ņ░© Ļ│Ąņ¦ä ļ¬©ļō£ņÖĆ 3ņ░© Ļ│Ąņ¦ä ļ¬©ļō£ļź╝ ņØ┤ņÜ®ĒĢ£ ņØ┤ņżæ ļīĆņŚŁ ņĀäĒīīĒØĪņłśņ▓┤ņŚÉ ļīĆĒĢ£ Ļ▓░Ļ│╝ņÖĆ ļÅÖņØ╝ĒĢśļŗż [26-28].
3.3. ņŗ£ĒÄĖ ņĀ£ņ×æ ļ░Å ņŗżņĖĪ
GPMAņØś ņĀäĒīīĒØĪņłśĒŖ╣ņä▒ņØä ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ PCB ņĀ£ņĪ░ Ļ│Ąļ▓ĢņŚÉ ņØśĒĢ┤ ĻĘĖļ”¼ļō£ ļÅäņ▓┤/FR4/ļ░░ļ®┤ ļÅäņ▓┤ ĒīÉļä¼ņØä ņĀ£ņ×æĒĢśĻ│Ā, ņ×Éņ£ĀĻ│ĄĻ░äļ▓ĢņŚÉ ņØśĒĢ┤ ļ░śņé¼ņåÉņŗżņØä ņŗżņĖĪĒĢśņśĆļŗż. ņŗ£ĒŚśņŗ£ĒÄĖ ņĀ£ņ×æ(ņÖĖļČĆ ņŚģņ▓┤ņŚÉ ņØśļó░) Ļ│╝ņĀĢņØĆ ļŗżņØīĻ│╝ Ļ░Öļŗż: (a) auto CADņŚÉ ņØśĒĢ£ Ēī©Ēä┤ ņäżĻ│ä, (b) ļĀłņØ┤ņĀĆ Ēöäļ”░Ēä░ļź╝ ņØ┤ņÜ®ĒĢ£ layout sheet ņØĖņćä, (c) ĒĢäļ”ä ņ£äņŚÉ Ēī©Ēä┤ layout ļ│Ąņé¼ ļ░Å Ēśäņāü, (d) positive photoresistļĪ£ ļÅäĒżļÉ£ PCB ļ░ĢĒīÉ ņ£äņŚÉ ĒĢäļ”äņØä ņĀĢļĀ¼ĒĢśĻ│Ā ņ×ÉņÖĖņäĀņŚÉ ļģĖĻ┤æ, (e) ļČĆņŗØņä▒ ņåīļŗż (NaOH) ņÜ®ņĢĪ ņåŹņŚÉņä£ PCB ļ░ĢĒīÉņØś Ēśäņāü ļ░Å ņäĖņĀĢ, (e) ņĢĮ 40 oCņŚÉņä£ 10% Ļ│╝ņé░ĒÖö ĒÖ®ņé░ ņĢöļ¬©ļŖäņØä ņé¼ņÜ®ĒĢśņŚ¼ ļ░ĢĒīÉņØä ņŚÉņ╣ŁĒĢśĻ│Ā ņäĖņĀĢ. ĻĘĖļ”╝ 5(a)ļŖö ņĖĪņĀĢ ņŗ£ĒÄĖņØś ņé¼ņ¦äņØ┤ļŗż. ņŗ£ĒÄĖņØś Ēü¼ĻĖ░ļŖö 50 ├Ś 50 cmņØ┤Ļ│Ā, 5 ├Ś 5 Ļ░£ņØś ļŗ©ņ£ä ņģĆņØä ĒżĒĢ©ĒĢ£ļŗż.
ĻĘĖļ”╝ 5(b)ļŖö ņĀäĒīīņĢöņŗż ņĢłņŚÉ ĻĄ¼ņä▒ļÉ£ ņĖĪņĀĢ ņŗ£ņŖżĒģ£ņØä ļ│┤ņŚ¼ņżĆļŗż. ļæÉ Ļ░£ņØś Ēś╝ ņĢłĒģīļéś, ĒÜīļĪ£ļ¦Ø ļČäņäØĻĖ░ (Agilent E8364B), ĻĘĖļ”¼Ļ│Ā ņĖĪņĀĢ ņŗ£ĒÄĖņ£╝ļĪ£ ĻĄ¼ņä▒ļÉ£ļŗż. ņÖäņĀä ļ░śņé¼ņ▓┤ņØĖ ĻĄ¼ļ”¼ĒīÉņ£╝ļĪ£ ļ│┤ņĀĢĒĢ£ ļŗżņØī, ņĖĪņĀĢ ņŗ£ĒÄĖņØś ņĀäļĀźļ░śņé¼ņ£©ņØä ņĖĪņĀĢĒĢśņśĆļŗż. Ēś╝ ņĢłĒģīļéśļŖö Schwarzbeck ņé¼ņØś BBHA 9120E ļ¬©ļŹĖļĪ£, ņĖĪņĀĢ ņŻ╝Ēīīņłś ļīĆņŚŁņØĆ 0.5 GHz ŌłÆ6 GHzņØ┤Ļ│Ā, ĒÅŁ = 424 mm, ļåÆņØ┤ = 314 mm, ĻĖĖņØ┤ = 820 mmņØś ņ╣śņłśļź╝ Ļ░Ćņ¦äļŗż. ļ░®ņé¼ Ēī©Ēä┤ņØĆ 30┬░ ĻĖ░ņżĆ, 1 GHzņŚÉņä£ ŌĆō10 dB, 2.5 GHzņŚÉņä£ ŌĆō20 dBņØś ļåÆņØĆ ņ¦ĆĒ¢źņä▒ņØä ļ│┤ņØĖļŗż. ņĢłĒģīļéśņØś ļ░®ņé¼ ļ░®Ē¢źņä▒ņŚÉ ļö░ļźĖ ņśżņ░©ļŖö Ļ▓Įņé¼ņ×ģņé¼ ņĖĪņĀĢņŚÉņä£ Ēü░ ļ¼ĖņĀ£Ļ░Ć ņŚåņØä Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
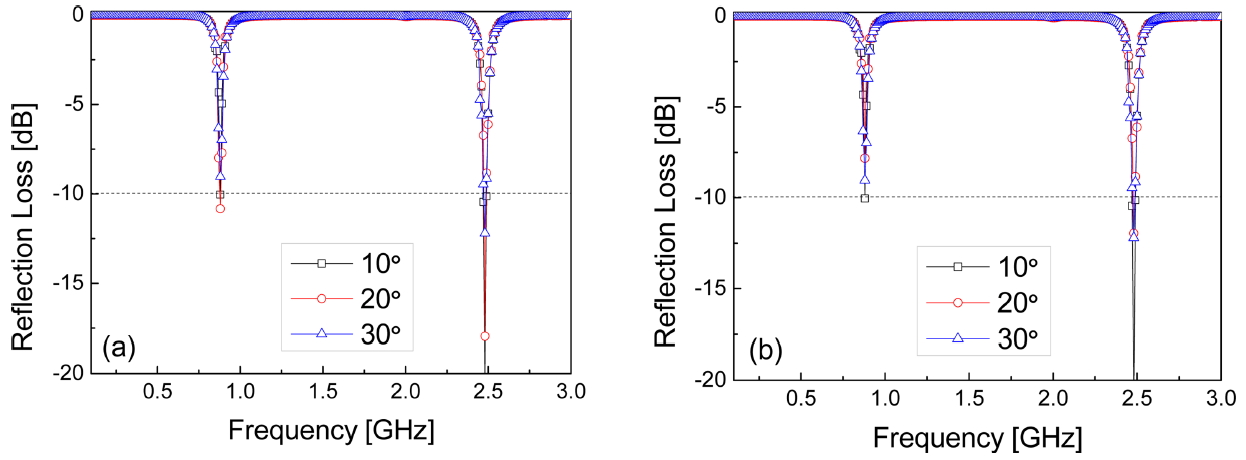
ĻĘĖļ”╝ 6ņØĆ GPMA ĒīÉļä¼ņØś ļ░śņé¼ņåÉņŗż ņĖĪņĀĢĻ▓░Ļ│╝ņØ┤ļŗż. ņ×ģņé¼Ļ░üņØ┤ ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ ļ░śņé¼ņåÉņŗżņØ┤ ņĢĮĻ░ä ņ”ØĻ░ĆĒĢśļŖö Ļ▓ĮĒ¢źņØä ļ│┤ņØ┤ļéś, TE, TM ĒÄĖĒīī ļ¬©ļæÉņŚÉņä£ ņ×ģņé¼Ļ░ü 30┬░Ļ╣īņ¦Ć f1 = 0.88 GHzņŚÉņä£ ŌĆō10 dB ņłśņżĆ, f2 = 2.48 GHzņŚÉņä£ ŌĆō12 dBņØś ņØ┤ĒĢśņØś ļ░śņé¼ņåÉņŗżņØä ļ│┤ņØĖļŗż. ĻĘĖļ”╝ 2ņØś ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ▓░Ļ│╝ņÖĆ ņל ņØ╝ņ╣śĒĢ©ņØä ļ│╝ ņłś ņ׳Ļ│Ā, Ļ▓Įņé¼ņ×ģņé¼ ĒŖ╣ņä▒ ļśÉĒĢ£ ņÜ░ņłśĒĢ©ņØä ļ│┤ņŚ¼ņżĆļŗż.
ļ®öĒāĆņåīņ×¼ņØś Ļ│Ąņ¦äĒŖ╣ņä▒ņŚÉ ņØśĒĢ┤ ĒØĪņłś ļīĆņŚŁĒÅŁņØ┤ ņóüņØĆ Ļ▓āņØ┤ ļ│Ė ņäżĻ│äņØś ļŗ©ņĀÉņØ┤ļŗż. ļīĆņŚŁĒÅŁņØä ĒÖĢļīĆĒĢĀ ņłś ņ׳ļŖö ļ░®ņĢłņ£╝ļĪ£ļŖö Ēü¼ĻĖ░Ļ░Ć ļŗżļźĖ ĻĘĖļ”¼ļō£ Ēī©Ēä┤ ļÅäņ▓┤ņØś ļŗżņżæĻ│Ąņ¦äņØä ņØ┤ņÜ®ĒĢśļŖö Ļ▓āņØä Ļ│ĀļĀżĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļŖö ļŗ©ņ£ä ņģĆ ņŻ╝ĻĖ░ ļśÉļŖö ĻĄ¼ņä▒ ļÅäņ▓┤ņØś ņĀüņĀłĒĢ£ Ēü¼ĻĖ░ ļ░░ĒĢ®ņŚÉ ņØśĒĢ┤ ĒØĪņłśļīĆņŚŁĒÅŁņØä ĒÖĢņןņŗ£Ēé© ņŚ░ĻĄ¼ ņé¼ļĪĆņŚÉ ĻĘ╝Ļ▒░ĒĢ£ļŗż [29-31].
4. Ļ▓░ ļĪĀ
RF-IDņØś ļÅÖņ×æ ņŻ╝ĒīīņłśņØĖ 0.8 GHz ļīĆņÖĆ 2.4 GHz ļīĆņŚÉņä£ ļ¬©ļæÉ ņé¼ņÜ® Ļ░ĆļŖźĒĢ£ ĻĘĖļ”¼ļō£ Ēī©Ēä┤ņØś ļ®öĒāĆņåīņ×¼ ĒØĪņłśņ▓┤ļź╝ HFSS ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ĒåĄĒĢśņŚ¼ ļÅäņČ£ĒĢśņśĆļŗż. ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ▓░Ļ│╝ 0.88 GHzņÖĆ 2.48 GHz ļ¬©ļæÉņŚÉņä£ ŌĆō10 dB ņØ┤ĒĢśņØś ļ░śņé¼ņåÉņŗżņØä ņ¢╗ņØä ņłś ņ׳ņŚłļŗż. ĒåĄņāüņĀüņØĖ PCB ņĀ£ņĪ░ Ļ│Ąļ▓ĢņŚÉ ņØśĒĢ┤ ĻĘĖļ”¼ļō£ ļÅäņ▓┤/FR4/ļ░░ļ®┤ ļÅäņ▓┤ ĒīÉļä¼ņØä ņĀ£ņ×æĒĢśĻ│Ā, ņ×Éņ£ĀĻ│ĄĻ░äļ▓ĢņŚÉ ņØśĒĢ┤ ļ░śņé¼ņåÉņŗżņØä ņŗżņĖĪĒĢ£ Ļ▓░Ļ│╝, ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ▓░Ļ│╝ņÖĆ ņל ņØ╝ņ╣śĒĢ©ņØä ĒÖĢņØĖĒĢśņśĆļŗż. TE ĒÄĖĒīīņÖĆ TM ĒÄĖĒīī ļ¬©ļæÉ ņĢĮ 30┬░Ļ╣īņ¦ĆņØś Ļ▓Įņé¼ņ×ģņé¼ņŚÉ ļīĆĒĢ┤ņä£ļÅä 10 dB ņłśņżĆņØś ĒØĪņłśļŖźņØä ņ£Āņ¦ĆĒĢśņśĆļŗż. ĻĖ░ņĪ┤ņØś UHF ļīĆņŚŁņÜ® ĒØĪņłśņ▓┤ņŚÉ ļ╣äĒĢ┤ ļ░ĢĒśĢĒÖö ļ░Å Ļ▓Įņé¼ņ×ģņé¼ ĒŖ╣ņä▒ņØ┤ Ēü¼Ļ▓ī Ļ░£ņäĀļÉ£ Ļ▓░Ļ│╝ņØ┤ļŗż. ļ│Ė ļģ╝ļ¼ĖņØś Ļ▓░Ļ│╝ļŖö grid pattern ļ®öĒāĆņåīņ×¼ļ¦īņØś dual band ĒØĪņłśņä▒ļŖźņØ┤ļŗż. ņØ┤ļź╝ RFID ņŗ£ņŖżĒģ£ ĻĘ╝ņ▓śņŚÉ ņäżņ╣śĒĢśņśĆņØä ļĢī ņĀäņ×ÉĒīī Ļ░äņäŁ ļ¼ĖņĀ£ ĒĢ┤ņåī ļ░®ņĢłņØś ĒĢśļéśļĪ£ ĒÖ£ņÜ®ĒĢĀ ņłś ņ׳ļŗżļŖö Ļ▓░Ļ│╝ ņĀ£ņŗ£ņØ┤ļŗż. ņŗżņĀ£ RFID ņŗ£ņŖżĒģ£, ļśÉļŖö ņŻ╝ļ│ĆņŚÉ ņØ┤ļź╝ ņĀüņÜ®Ē¢łņØä ļĢī ņĀäņ×ÉĒīī ĒÜ©Ļ│╝ ņĖĪņĀĢņØĆ ņŗ£ņŖżĒģ£ ņ░©ņøÉņŚÉņä£ ļśÉ ļŗżļźĖ ņŚ░ĻĄ¼ļź╝ ņÜöĒĢ£ļŗż.