1. INTRODUCTION
Tetrahedrite is an abundant natural material in the earth and has recently attracted considerable attention as a p-type thermoelectric material for mid-temperature applications. Synthetic tetrahedrite (Cu12Sb4S13) exhibits good thermoelectric performance near 723 K [1,2]. Cu12Sb4S13 has a complex crystal structure with 58 atoms arranged in a highly symmetric cubic unit cell composed of CuIS4 tetrahedra, CuIIS3 triangles, and SbS3 trigonal pyramids [3]. The most prominent characteristic of tetrahedrite is its low thermal conductivity. Because of the active lone-pair electrons of the Sb atoms, CuII atoms in a plane S triangle induce low lattice thermal conductivity by anharmonic oscillation with low frequency and high amplitude [4-6]. Thermoelectric conversion efficiency is evaluated using a dimensionless figure of merit (ZT) defined as ZT = α2σκ-1T, where α, σ, κ, and T are the Seebeck coefficient, electrical conductivity, thermal conductivity, and absolute temperature, respectively. Good thermoelectric materials need to have a high Seebeck coefficient, high electrical conductivity, and low thermal conductivity, however, the Seebeck coefficient and electrical conductivity have a trade-off relationship to the power factor. In general, the power factor can be improved by optimizing the carrier concentration through doping.
Most studies on tetrahedrites have focused on the substitution of transition elements (Zn, Fe, Ni, etc.) for Cu sites [7-9], but few studies have reported on the effects of doping for Sb sites. In this approach, the Sb site of the natural mineral tetrahedrite is partially replaced by As, Bi, or Te atoms. Studies on the substitution of Sb sites in synthetic tetrahedrite have been reported. Kumar et al. [10] reported on Bi-doped Cu12Sb4-yBiyS13 prepared by encapsulated melting and hot pressing (HP). As the amount of Bi increased, both the carrier concentration (electrical conductivity) and thermal conductivity decreased. As a result, a ZT of 0.84 was obtained at 673 K for Cu12Sb3.9Bi0.1S13. Bouyrie et al. [11] studied Te-doped Cu12Sb4-yTeyS13 synthesized by encapsulated melting and spark plasma sintering. As the content of Te increased, the carrier concentration and thermal conductivity decreased, and thus a ZT of 0.8 was achieved at 623 K for Cu12Sb3.39Te0.61S13
In general, when tetrahedrite is synthesized using a melting process, sophisticated and slow reactions (heating–holding– cooling) are required because the boiling point (717.8 K) of S is considerably lower than the melting point (1356.6 K) of Cu. In addition, a long-time heat treatment is required for phase transformation and homogenization. In this regard, mechanical alloying (MA) has several advantages over conventional melt-crushing techniques, including the prevention of phase separation and vaporization during melting. MA has been previously employed in the synthesis of nanosized powders. In our previous study, a single tetrahedrite phase was successfully synthesized in a short time using the MA method [12]. In this study, Bi-doped tetrahedrites Cu12Sb4-yBiyS13 were prepared by MA and HP, and their thermoelectric properties were examined. By partially substituting Bi for the Sb sites of the tetrahedrite, we expected an enhanced power factor and reduced thermal conductivity, and improved thermoelectric performance by optimizing the carrier concentration.
2. EXPERIMENTAL PROCEDURE
Bi-doped tetrahedrites Cu12Sb4-yBiyS13 (y = 0.1-0.4) were synthesized by MA. Cu (purity 99.9%, < 45 μm, Kojundo), Sb (purity 99.999%, < 150 μm, Kojundo), Bi (purity 99.999%, < 180 μm, Kojundo), and S (purity 99.99%, < 75 μm, Kojundo) were weighed to the stoichiometric composition. The mixed powder was charged into a hardened stainlesssteel jar with stainless-steel balls having diameters of 5 mm, where the ball-to-powder weight ratio was 20. MA was performed at 350 rpm for 24 h in an Ar atmosphere using a planetary mill (Fritsch Pulverisette5). The synthesized powder was loaded into a graphite mold having an inner diameter of 10 mm and subjected to consolidation using HP at 723 K for 2 h under 70 MPa in vacuum. Details of the MA-HP process for the solid-state synthesis of tetrahedrite are described in the previous study [12].
The phases of the MA powders and HP specimens were analyzed using X-ray diffraction (XRD; Bruker D8-Advance) with Cu-Kα radiation (λ = 0.15405 nm). The diffraction patterns were measured in the θ–2θ mode (2θ = 10–90°) with a step size of 0.02° at a scan speed of 0.4 s/step. The fractured surfaces of the HP specimens were observed using scanning electron microscopy (SEM; FEI Quanta400), and elemental analysis was conducted using energy-dispersive spectrometry (EDS; Bruker Quantax200). The energy levels of the elements were Cu-Lα (0.928 eV), Sb-Lα (3.604 eV), Bi-Mα (2.423 eV), and S-Kα (2.309 eV). The sintered body was cut into a rectangular parallelepiped of 3 × 3 × 9 mm to measure the Seebeck coefficient and electrical conductivity. It was then further cut into a disk of 10 mm (diameter) × 1 mm (thickness) for thermal conductivity measurement. Thermoelectric properties were examined in the temperature range of 323 to 723 K. The Seebeck coefficient and electrical conductivity were measured using the temperature-differential and DC four-probe method in a He atmosphere (Ulvac-Riko ZEM-3). The thermal conductivity was obtained by the laser flash method (Ulvac-Riko TC-9000H) after thermal diffusivity, specific heat, and density were measured. Finally, the power factor (PF = α2σ) and the ZT (= α2σκ-1T) were evaluated.
3. RESULTS AND DISCUSSION
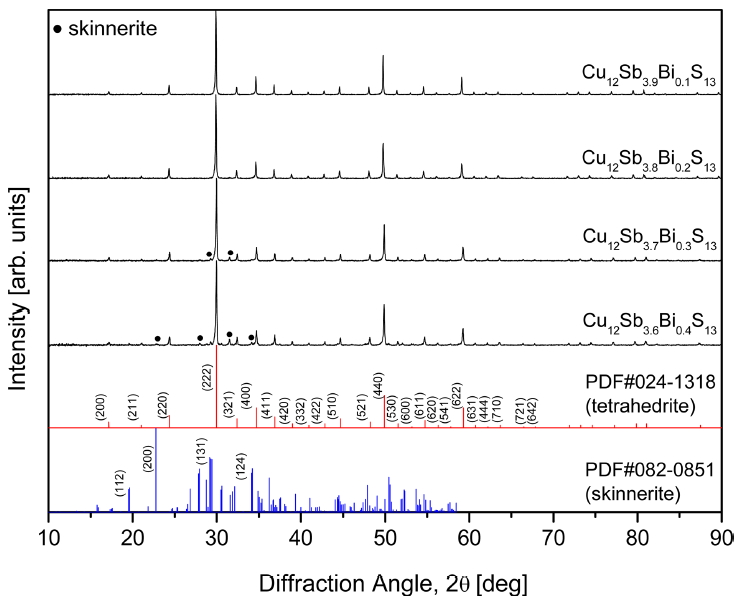
Figure 1 shows the XRD patterns of Cu12Sb4-yBiyS13 synthesized by MA and sintered by HP. The diffraction peaks of all specimens matched the standard diffraction data (PDF#024-1318, space group I4 ¯
Figure 2 presents SEM images of the fractured surfaces of Cu12Sb4-yBiyS13. Densely sintered bodies were obtained with high relative densities of 97.9-99.2%. No significant change was found in the microstructure due to the Bi substitution. Figure 3 shows the EDS elemental maps of the Cu12Sb3.9Bi0.1S13 from a typical specimen with uniform distribution of constituent elements. Table 1 shows that Cu and Sb contents were higher and S content was lower than the nominal composition. As mentioned in our description of the experimental method, because the energy levels of Bi and S used in the EDS analysis are similar, measurement errors might be high. However, in our previous studies [12-14] on non-doped and doped tetrahedrites prepared by the same MA-HP process, the actual compositions were similar to the nominal compositions.
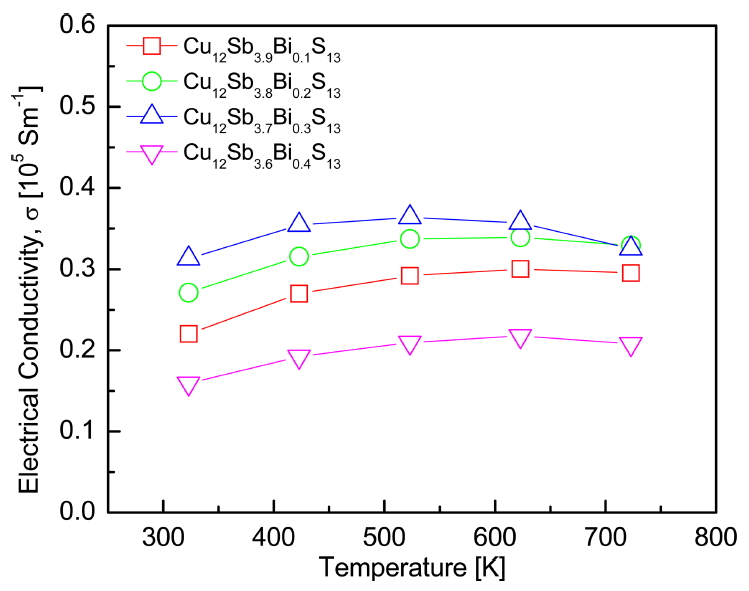
Figure 4 shows the electrical conductivity of Cu12Sb4yBiyS13. The electrical conductivity increased with increasing temperature in all specimens and then decreased at temperatures higher than 623 K. This was thought to be because of the change in conduction behavior with temperature. Tetrahedrites usually show a metallic-to-semiconductor transition, which corresponds to the movement of the Fermi level from inside the valence band to the mid-gap [15]. The electrical conductivity increased as the amount of Bi increased. However, it might be unusual to expect that the substitution of Bi for the Sb site would not induce changes in the carrier concentration and electrical conductivity because Bi and Sb are isovalent. Li et al. [16] reported that lattice distortion and point defects (Cu vacancies) were formed in Bi-doped permingeatites Cu3Sb1yBiySe4 because of Bi substitution, which has a larger radius than Sb. Cu vacancies acted as acceptors, which was related to the high hole concentration of tetrahedrite [17,18]. The specimen with y = 0.4 showed lower electrical conductivity than Cu12Sb3.9Bi0.1S13. This was believed to be because of secondary-phase Cu3SbS3. Kumar et al. [10] reported that the secondary phase can reduce carrier mobility and increase electrical resistivity by charge carrier scattering.
Figure 5 presents the Seebeck coefficient of Cu12Sb4yBiyS13. All specimens showed positive values for the Seebeck coefficient. The Seebeck coefficient of a p-type semiconductor is expressed as α = (8/3)π2k2Bm*Te-1h-2(π/3n)2/3, where kB is the Boltzmann constant, h is the Planck constant, m* is the effective carrier mass, e is the electronic charge, n is the carrier concentration, and T is the absolute temperature [19]. In general, as the temperature increases, the Seebeck coefficient increases, but at a certain temperature or higher, an intrinsic transition occurs and the carrier concentration increases rapidly. Therefore, the contribution to the decrease in the Seebeck coefficient becomes greater than the increase in carrier concentration as the temperature rises, and then the Seebeck coefficient decreases after reaching a peak value. In this study, the temperature dependence of the Seebeck coefficient was similar for all specimens and no intrinsic transition occurred up to 723 K. Because the Seebeck coefficient is inversely related to the carrier concentration, a higher Seebeck coefficient was obtained at a lower Bi content. However, the Cu12Sb3.6Bi0.4S13 specimen showed a higher Seebeck coefficient than the Cu12Sb3.7Bi0.3S13 specimen, possibly because of the secondary phase, which had the lowest electrical conductivity, as shown in Fig 4.
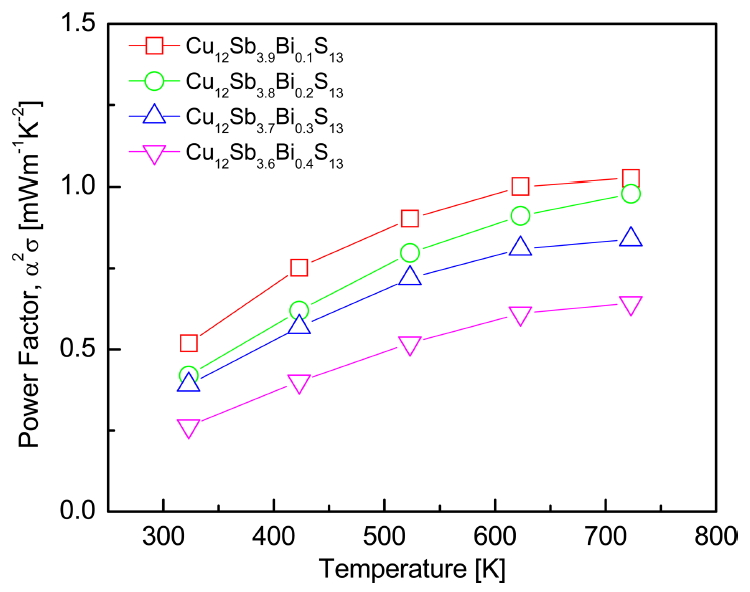
Figure 6 shows the power factor of Cu12Sb4-yBiyS13. As the temperature increased, the power factor increased. This occurred because of the temperature dependence of the electrical conductivity and the Seebeck coefficient. As the Bi amount increased, the power factor decreased because the decrease in the Seebeck coefficient dominated the increase in the electrical conductivity. Undoped Cu12Sb4S13 showed a maximum PF = 1.0 mWm-1K-2 at 723 K [12], but the power factor of Cu12Sb3.9Bi0.1S13 slightly increased to PF = 1.02 mWm-1K-2 at 723 K. Kumar et al. [10] obtained PF = 1.5 mWm-1K-2 at 673 K for Cu12Sb3.8Bi0.2S13 because of the increase in the Seebeck coefficient produced by Bi doping. This demonstrates the partial substitution of Bi for Sb sites is effective at increasing the power factor of tetrahedrite.
Figure 7 presents the thermal conductivity of Cu12Sb4yBiyS13. The thermal conductivity is the sum of the electronic thermal conductivity (κE) of charge carrier contributions and the lattice thermal conductivity (κL) of phonon contributions. The electronic thermal conductivity was calculated using the Wiedemann–Franz law (κE = LσT, L: Lorenz number) [20]. The Lorenz number can be obtained using the relation L [10-8 V2K-2] = 1.5 + exp(-|α|/116) [21], as shown in Table 1. In Fig 7(a), the thermal conductivity slightly increased as the amount of doped Bi increased in all samples except for that of y = 0.4. The specimen with y = 0.4 showed the lowest thermal conductivity of 0.63 Wm-1K-1 at 723 K, but this was expected to be due to additional phonon scattering by the secondary phase. Kumar et al. [10] achieved the lowest thermal conductivity of 0.98Wm-1K-1 at 673K for Cu12Sb3.6Bi0.4S13. The tetrahedrite induces inherently low thermal conductivity, and Cu atoms lower the lattice thermal conductivity through phonon scattering to bring the lattice thermal conductivity close to the theoretical minimum value [22]. Figure 7(b) shows that the electronic and lattice thermal conductivities were less than 0.40 Wm-1K-1 and 0.66 Wm-1K-1, respectively, for all samples over the entire temperature range. The electronic thermal conductivity was in agreement with the tendency of the electrical conductivity to increase with increasing Bi doping content, which was influenced by the increase in carrier concentration.
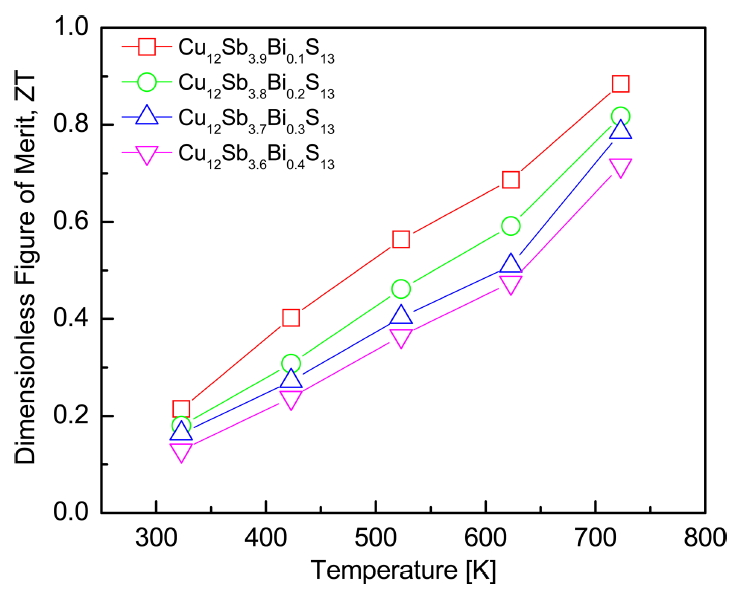
Figure 8 shows the dimensionless figure of merit (ZT) of Cu12Sb4-yBiyS13. The ZT value increased with increasing temperature, and a maximum value of ZTmax = 0.88 was obtained at 723 K for Cu12Sb3.9Bi0.1S13 with a high power factor (1.02 mWm-1K-2) and low thermal conductivity (0.81 Wm-1K-1). However, the ZT value decreased as the doping level of Bi increased. In the previous study [12], the undoped Cu12Sb4S13 prepared under the same conditions exhibited ZTmax = 0.86 at 723 K. Barbier et al. [23] obtained ZTmax = 0.60 at 723 K for Cu12Sb4S13 synthesized by encapsulated melting and spark plasma sintering. Kumar et al. [10] reported ZTmax = 0.84 at 673 K for Cu12Sb3.8Bi0.2S13 fabricated by encapsulated melting and HP. Therefore, the partial substitution of Bi for Sb sites by the MA-HP process was successful and effective for improving ZT of tetrahedrite.
4. CONCLUSION
Bi-doped tetrahedrites Cu12Sb4-yBiyS13 (y = 0.1-0.4) were synthesized by MA and sintered by HP. A single tetrahedrite phase was obtained, but specimens with y ≥ 0.3 had a small amount of the secondary phase (skinnerite). The lattice constant was increased by Bi doping because Bi is larger than Sb, and Bi was confirmed to be substituted for Sb sites. As the Bi doping level increased, the electrical conductivity increased, but the Seebeck coefficient decreased. This occurred because of the increase in carrier concentration. As a result, a maximum power factor of 1.02 mWm-1K-2 was achieved at 723 K for Cu12Sb3.9Bi0.1S13. All specimens showed very low thermal conductivity below 0.96 Wm-1K-1 at temperatures in the range of 323 to 723 K. Consequently, ZTmax = 0.88 was obtained at 723 K for Cu12Sb3.9Bi0.1S13, which had a high power factor and no secondary phase.